Тишин В. И.
Решения вариантов
письменных работ,
Предлагаемых на
Вступительных экзаменах
В Брянские вузы
В 1997 - 2000 гг.
Брянск
Г.
Содержание
Варианты письменных работ. 5
Вариант 1. 5
Вариант 2. 5
Вариант 3. 6
Вариант 4. 6
Вариант 5. 7
Вариант 6. 7
Вариант 7. 8
Вариант 8. 8
Вариант 9. 9
Вариант 10. 9
Вариант 11. 10
Вариант 12. 10
Вариант 13. 11
Вариант 14. 11
Вариант 15. 12
Вариант 16. 12
Вариант 17. 13
Вариант 18. 14
Вариант 19. 14
Вариант 20. 15
Решения
Вариант 1. 16
Решения. 16
Вариант 2. 24
Решения. 24
Вариант 3. 29
Решения. 30
Вариант 4. 35
Решения. 35
Вариант 5. 42
Решения. 42
Вариант 6. 48
Решения. 48
Вариант 7. 54
Решения. 54
Вариант 8. 60
Решения. 61
Вариант 9. 67
Решения. 68
Вариант 10. 73
Решения. 73
Вариант 11. 79
Решение. 79
Вариант 12. 86
Решения. 87
Вариант 13. 94
Решения. 95
Вариант 14. 101
Решения. 101
Вариант 15. 106
Решения. 106
Вариант 16. 112
Решения. 112
Вариант 17. 117
Решения. 118
Вариант 18. 123
Решения. 123
Вариант 19. 132
Решения. 132
Вариант 20. 140
Решения. 140
Варианты письменных работ
В Брянскую государственную инженерно-технологическую академию
На репетиционных экзаменах в 1997 году
Вариант 1
1. Упростить: 
2. Решить уравнение: 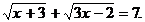
3. Укажите все значения x, для которых

является действительным числом.
4. Решить уравнение: 
5. Окружность, вписанная в треугольник, делит одну из медиан на 3 равные части. Найти отношение длин сторон треугольника.
6. В правильной шестиугольной пирамиде длина апофемы боковой грани 5 см. При какой длине сторон основания объем пирамиды будет наибольшим?
7. Решить уравнение: 
Вариант 2
1. Упростить выражение: 
2. Решить уравнение: 
3. Найти область определения функции:

4. Решить уравнение: 
5. Решить уравнение: 
6. Найти сторону тетраэдра, вписанного в шар радиуса R.
7. На кривой  найдите точку, расстояние которой до прямой
найдите точку, расстояние которой до прямой 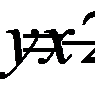 будет наименьшим.
будет наименьшим.
Вариант 3
1. Упростить: 
2. Решить уравнение: 
3. Найти область определения функции:
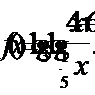
4. Решить уравнение: 
5. Решить уравнение: 
6. Окружность проходит через вершины B, C, D трапеции ABCD и касается стороны AB в точке B. Найти длину диагонали BD, если длины оснований равны a и b.
7. Объем правильной треугольной призмы равен 16 дм3. Каковы должны быть основания и высота, чтобы площадь полной поверхности призмы была наименьшей?
Вариант 4
1. Упростить: 
2. Решить систему: 
3. Найти область определения функции:
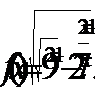
4. Решить уравнение: 
5. Решить уравнение: 
6. В основании пирамиды лежит ромб. Высота пирамиды проходит через центр ромба. Боковые грани пирамиды образуют углы 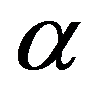 и
и  с диагоналями ромба. Найти угол наклона боковой грани к плоскости основания.
с диагоналями ромба. Найти угол наклона боковой грани к плоскости основания.
7. Найти высоту конуса максимального объема, который можно вписать в шар радиуса R.
Вариант 5
1. Упростить: 
2. При каких значениях a разность корней уравнения 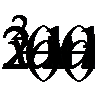 равна их произведению?
равна их произведению?
3. Решить неравенство: 
4. Решить уравнение 
5. Решить уравнение: 
6. Два экскаватора производят работу. Если эту работу будет выполнять один первый экскаватор, то он может закончить ее на 8 ч. позже, чем оба вместе. Если эту работу будет выполнять один второй экскаватор, то он закончит ее на 4,5 ч позже, чем оба вместе. За какое время может выполнить эту работу каждый экскаватор в отдельности?
7. Стороны треугольника, лежащего в основании пирамиды равны 13, 14, 15 см. Двугранные углы при основании пирамиды равны по 450. Найти боковую поверхность пирамиды.
Вариант 6
1. Упростить: 
2. Решить неравенство: 
3. Решить уравнение: 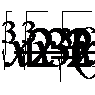
4. Решить уравнение: 
5. Доказать тождество 
6. Образующая усеченного конуса наклонена к его основанию, имеющему радиус R, под углом 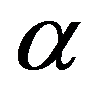 ; радиус другого основания равен r. Определить боковую поверхность усеченного конуса.
; радиус другого основания равен r. Определить боковую поверхность усеченного конуса.
7. В круг радиуса r вписать прямоугольник с наибольшей площадью.
Вариант 7
1. Упростить: 
2. Найти все решения уравнения  , принадлежащих области определения функции
, принадлежащих области определения функции 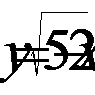
3. Решить уравнение: 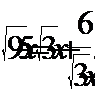
4. Решить уравнение: 
5. Решить уравнение: 
6. Два пешехода вышли одновременно навстречу друг другу и встретились через 3 ч. 20 мин. За какое время пройдет всё расстояние каждый из них, если первый пришел в то место, из которого вышел второй на 5 ч позже, чем второй пришел в то место, откуда вышел первый?
7. Основанием четырехугольной пирамиды служит ромб со стороной длины a и острым углом  . Каждая боковая грань наклонена к плоскости основания под углом
. Каждая боковая грань наклонена к плоскости основания под углом  Найти полную поверхность пирамиды.
Найти полную поверхность пирамиды.
Вариант 8
1. Упростить:
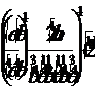
2. Решить аналитически и графически уравнение:

3. Решить уравнение: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Пункт C расположен в 12 км от B вниз по течению реки. Рыбак отправился на лодке в пункт C из пункта A, расположенного выше пункта B. Через 4 часа он прибыл в C, а на обратный путь затратил 6 часов. Поставив мотор и тем самым увеличив скорость лодки относительно воды втрое, рыбак дошел от A до B за 45 минут. Определить скорость течения реки.
7. Найти конус наименьшего объема, описанный около шара радиуса R.
Вариант 9
1. Упростить: 
2. Найти все решения уравнения  принадлежащие области допустимых значений функции
принадлежащие области допустимых значений функции

3. Решить уравнение: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Лодка спустилась вниз по течению реки на 20 км., затем вернулась обратно, затратив 7 ч. На обратном пути на расстоянии 12 км. от начального пункта лодка поравнялась с плотом, который проплывал пункт отплытия лодки в момент ее отплытия. Определить скорость течения реки и скорость движения лодки вниз по течению.
7. Основанием пирамиды служит ромб, длины диагоналей которого равны 6 м и 8 м. Высота пирамиды проходит через точку пересечения диагоналей ромба и имеет длину 1 м. Найти площадь боковой поверхности пирамиды.
Вариант 10
1. Упростить:

2. Пусть  и
и  корни уравнения
корни уравнения  Вычислить
Вычислить 
3. Решить неравенство: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Из двух городов выехали одновременно навстречу друг другу два автомобиля. Первый за 3 ч прошел 0,08 всего расстояния между городами, а второй за 2,5 ч. 7/120 этого расстояния. Найдите (в км/ч) скорость второго автомобиля, если до места встречи первый прошел 800 км.
7. Боковая грань правильной треугольной пирамиды образует с плоскостью основания угол 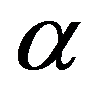 , сумма длин высоты пирамиды и радиуса окружности, вписанной в основание пирамиды равна a. Найти объем пирамиды.
, сумма длин высоты пирамиды и радиуса окружности, вписанной в основание пирамиды равна a. Найти объем пирамиды.
Вариант 11
1. Упростить выражение: 
2. Решить уравнение: 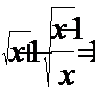
3. Найти область определения функции:

4. Решить уравнение: 
5. Решить уравнение: 
6. Отношение оснований равнобедренной трапеции равно m. Найти отношение радиусов окружностей, описанной около трапеции и вписанной в нее.
7. Определить размеры открытого бассейна объемом 32 см3 с квадратным дном, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Вариант 12
1. Упростить выражение:
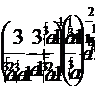
2. Решить аналитически и графически уравнение:

3. Решить уравнение: 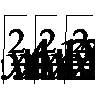
4. Решить уравнение: 
5. Решить уравнение: 
6. Два велосипедиста выехали одновременно из одного пункта в одном направлении. Первый из них ехал со скоростью 15 км/ч, а второй - со скоростью 12 км/ч. Спустя полчаса из того же пункта в том же направлении выехал третий велосипедист, который через некоторое время догнал второго, а еще через 1 ч. 30 мин. догнал и первого. Найти скорость третьего велосипедиста.
7. Найти радиус основания r и высоту h прямого кругового конуса, вписанного в шар радиуса R так, чтобы его объем был наибольшим.
Вариант 13
1. Упростить выражение: 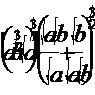
2. Решить систему: 
3. Решить неравенство: 
4. Решить уравнение: 
5. Решить уравнение: 
6. В равнобочную трапецию, длины оснований которой a и b (a > b), можно вписать окружность. Найти расстояние между центрами вписанной и описанной окружностей.
7. Какую наименьшую площадь может иметь треугольник, на гипотенузе которого лежит точка M(2; 1), а катеты - отрезки координатных осей.
Вариант 14
1. Упростить: 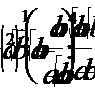
2. Решить уравнение: 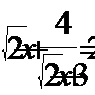
3. Решить неравенство: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Найти площадь треугольника, если длины двух его сторон равны 1 см. и  см., а длина медианы третьей стороны равна 2 см.
см., а длина медианы третьей стороны равна 2 см.
7. Группа студентов решила купить магнитофон ценой от 170 тыс. руб. до 195 тыс. руб. Однако, в последний момент двое отказались участвовать в покупке, поэтому каждому из остальных пришлось внести на 1 тыс. руб. больше. Сколько стоил магнитофон?
Вариант 15
1. Упростить: 
2. Решить неравенство: 
3. Решить уравнение: 
4. Решить уравнение: 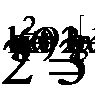
5. Доказать тождество: 
6. Угол при вершине сечения прямого кругового конуса равен  , а его высота равна h. Определить радиус шара, вписанный в конус.
, а его высота равна h. Определить радиус шара, вписанный в конус.
7. Найти размеры конической палатки данной вместимости, требующей наименьшее количество материала.
Вариант 16
1. Упростить: 
2. Решить уравнение: 
3. Найти область определения функции: 
4. Решить уравнение: 
5. Решить уравнение: 
6. Найти радиус шара вписанного в тетраэдр со стороной a.
7. На параболе  найти точку, расстояние от которой до точки M(9; 3) будет наименьшим.
найти точку, расстояние от которой до точки M(9; 3) будет наименьшим.
Вариант 17
1. Три числа составляют геометрическую прогрессию. Если от третьего отнять 4, то числа составят арифметическую прогрессию. Если же от второго и третьего числа полученной арифметической прогрессии отнять 1, то снова получится геометрическая прогрессия.
2. Решить уравнение:

3. Пешеход и велосипедист отправляются одновременно из пункта A в пункт B. В пункте B велосипедист поворачивает обратно и встречает пешехода через 20 минут после начала движения. Не останавливаясь, велосипедист доезжает до пункта A, поворачивает обратно и догоняет пешехода через 10 минут после первой встречи. За какое время пешеход пройдет путь от A до B?
4. Упростить выражение:


5. Решить уравнение: 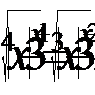
6. К окружности с центром в точке O проведены касательные AB и AC. M - точка пересечения луча OA с окружностью, DE - отрезок касательной, проведенной через точку M, заключенный между AB и AC. Определить |DE|, если |AO| = 39 см и радиус окружности равен 15 см.
7. При каких значениях p оба корня квадратного трехчлена

отрицательны?
Вариант 18
1. Три числа образуют геометрическую прогрессию. Если второе число увеличить на 2, то прогрессия станет арифметической, а если после этого, увеличить последнее число на 9, то прогрессия снова станет геометрической. Найти числа.
2. Решить уравнение: 
3. Пристань A находится выше течению реки, чем пристань B. Из A в B одновременно навстречу друг другу начинают движение плот и моторная лодка. Достигнув пристани A моторная лодка немедленно повернула обратно и догнала плот в тот момент, когда он прошел  расстояния между A и B. Найти время движения плота от A до B, если моторная лодка проплывает путь из B в A и обратно за 3 ч.
расстояния между A и B. Найти время движения плота от A до B, если моторная лодка проплывает путь из B в A и обратно за 3 ч.
4. Упростите 
5. Решить уравнение 
6. В полукруг, радиус которого 1 дм вписана трапеция, так что одно ее основание - диаметр полукруга. Найти площадь трапеции, если периметр ее равен 5 дм.
7. При каких значениях m корни уравнения  заключены в промежутке между -1 и 2?
заключены в промежутке между -1 и 2?
Вариант 19
1. При каких значениях a наименьшее значение функции

равно –4.
2. Решить и исследовать неравенство: 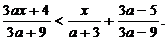
3. При всех значениях параметра a решить систему:

4. Найти все значения параметра a, для которых квадратные уравнения  имеют, по крайней мере, один общий корень.
имеют, по крайней мере, один общий корень.
5. При каких значениях p корни уравнения 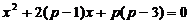 имеют разные знаки?
имеют разные знаки?
6. 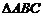 задан координатами вершин A(1; -1; 5), B(3; 4; 4), C(4; 6; 1). На плоскости xOy найти точку, проекцией которой на плоскости ABC служит центр описанной около
задан координатами вершин A(1; -1; 5), B(3; 4; 4), C(4; 6; 1). На плоскости xOy найти точку, проекцией которой на плоскости ABC служит центр описанной около 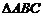 окружности.
окружности.
7. Найти площадь равнобедренной трапеции, если высота равна h, а боковая сторона видна из центра описанной окружности под углом  .
.
Вариант 20
вступительного экзамена по математике 21.07.1997 г.
1. Решить уравнение 
2. Решить неравенство 
3. Решить уравнение 
4. Решить уравнение 
5. Найти все значения p, при которых уравнение  не имеет корней.
не имеет корней.
6. В конус вписана пирамида,  В основании пирамиды лежит треугольник с углами
В основании пирамиды лежит треугольник с углами 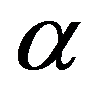 и
и  . Найти объем конуса.
. Найти объем конуса.
Вариант 1
1. Упростить: 
2. Решить уравнение: 
3. Укажите все значения x, для которых
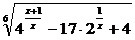
является действительным числом.
4. Решить уравнение: 
5. Окружность, вписанная в треугольник, делит одну из медиан на 3 равные части. Найти отношение длин сторон треугольника.
6. В правильной шестиугольной пирамиде длина апофемы боковой грани 5 см. При какой длине сторон основания объем пирамиды будет наибольшим?
7. Решить уравнение: 
Решения
1. Упростить:

Решение
Наложим ограничения на переменную величину x. Выражение будет иметь смысл, если  и
и  т. е.
т. е. 
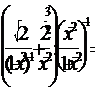
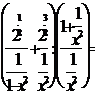
= 
Ответ:  , при
, при  и
и 
2. Решить уравнение: 
Решение
1-й способ
Найдем область допустимых значений
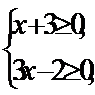



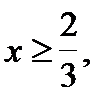

Возведем обе части уравнения в квадрат










