учитывая область допустимых значений 
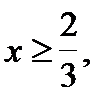получаем множество, на котором будем рассматривать полученное уравнение: 
Возведем, на этом промежутке, обе части полученного уравнения в квадрат, получим
- не входит в промежуток 
и не является корнем уравнения.
входит в промежуток и является корнем уравнения.
Проверка
При x = 6 получим, 
значит x = 6 корень уравнения.
Ответ: 
2-й способ
Положим 
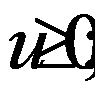
тогда 
умножим обе части первого уравнения на -3 и сложим со вторым уравнением, получим 
При такой подстановке заданное уравнение примет вид 
Получим систему уравнений
не является корнем, так как 
значит 
Ответ:
3. Укажите все значения 
для которых 
является действительным числом.
Решение
Выражение, находящееся под корнем четной степени, должно быть неотрицательным 
кроме того, переменная 
находится в знаменателе дроби, значит 
Решим первое показательное неравенство
Положим 
получим неравенство
Полученное неравенство, решим методом промежутков, учитывая, что 
(см. рисунок 1).
Рис. 1
и 
Делая обратную подстановку, получаем 
Это неравенство решим методом промежутков (см. рисунок 2):
Рис. 2
Получаем 
Это неравенство также решим методом промежутков (см. рисунок 3):
Рис. 3
отсюда находим 
Окончательно получаем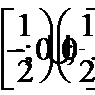 
Ответ: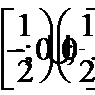
4. Решить уравнение: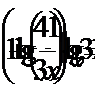 
Решение
Выражение, находящееся в основании логарифмической функции, должно быть положительным 
кроме того, необходимо проверить, может ли принимать значение, равное 1.
При 
получаем 
тогда логарифм по основанию 1 становится неопределенным 
значит 
Получим систему неравенств
Преобразуем уравнение
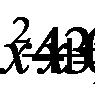
- не входит в область допустимых значений и не является корнем уравнения, 
входит в область допустимых значений.
Проверка
При x = 3 получим 
значит x = 3 является корнем уравнения.
Ответ: 
5. Окружность, вписанная в треугольник, делит одну из медиан на 3 равные части. Найти отношение длин сторон треугольника.
Решение
Рис. 4
1. Пусть ABC - данный треугольник, BM - медиана, значит CM = MA.
Обозначим BN = NL = LM = a. Отрезок касательной CP обозначим через x (см. рисунок 4).
2. Из вершины B проведены к окружности касательная BD и секущая BL. Применим теорему: "Квадрат касательной равен произведению секущей на ее внешний отрезок", значит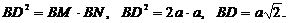 
Из точки M проведены касательная MP и секущая MN, тогда, по этой же теореме: 
3. Из точки B к окружности проведены две касательные BD и BK, по теореме: "Отрезки касательных, проведенных из одной точки к окружности равны", заключаем, что 
4. 
Снова, рассмотрим две касательные, проведенные из точки A: 
но
5. Теперь можно выразить все стороны треугольника через a и x:
6. Известно, что медиана треугольника выражается через его стороны по следующей формуле:
Подставим значения сторон и найдем x из полученного уравнения:
7. 
8. Теперь найдем искомое отношение сторон:
Ответ: 
6. В правильной шестиугольной пирамиде длина апофемы боковой грани 
При какой длине сторон основания объем пирамиды будет наибольшим?
Решение
Рис. 5
1. Проведем 
т. е. к плоскости основания, 
- высота пирамиды. 
- центр описанной и вписанной окружностей, так как пирамида правильная (см. рисунок 5).
Проведем 
и соединим 
с 
тогда 
по теореме о трех перпендикулярах, значит 
- апофема.
- радиус описанной окружности, который равен длине стороны правильного шестиугольника, 
Точка 
делит сторону 
пополам, так как 
равносторонний, отсюда 
Пусть - длина стороны шестиугольника, тогда 
Из 
по теореме Пифагора 
2. Из 
по теореме Пифагора 
3. Объем пирамиды равен
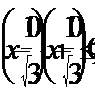
4. Рассмотрим объем, как функцию от на промежутке 
и найдем ее наибольшее значение на этом промежутке.
Найдем производную функции и критические точки, принадлежащие промежутку
Найдем критические точки на промежутке (В точке 
производная не существует, значит, она также является критической точкой).
и 
не входят в промежуток
Значит, остается исследовать поведение функции в точках 
и 
При 
- функция на этом промежутке возрастает.
При 
- функция на этом промежутке убывает.
В точке функция имеет максимум.
В точке 
объем равен нулю, поэтому наибольшее значение объем принимает при .
Ответ: наибольший объем при длине стороны см.
7. Решить уравнение: 
Решение
Преобразуем разность синусов 
в произведение, получим
С учетом этого преобразования, уравнение примет вид
Ответ: 
Вариант 2
1. Упростить выражение: 
2. Решить уравнение: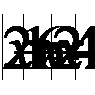 
3. Найти область определения функции:
4. Решить уравнение: 
5. Решить уравнение: 
6. Найти сторону тетраэдра, вписанного в шар радиуса R.
7. На кривой 
найдите точку, расстояние которой до прямой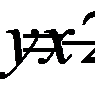 
будет наименьшим.
Решения
1. Упростить выражение: 
Решение
Как видим, это выражение имеет смысл, если 
и 
Ответ: 2, при и
2. Решить уравнение: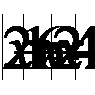
Решение
Найдем значения переменной x, при которых каждый из модулей обращается в нуль: 
Отметим эти точки на числовой прямой (см. рис. 6):
Рис. 6
Все множество действительных чисел разбивается этими точками на три промежутка: 
Решим уравнение на каждом из этих промежутков.
1. При 
оба выражения 2x - 1 и 2x - 4 принимают отрицательные значения и "выйдут" из под модулей со знаками "минус", значит, получим уравнение: 
- это значение входит в рассматриваемый промежуток и является корнем уравнения.
2. При 
выражение 2x - 1 будет принимать положительные значения и "выйдет" из под модуля со знаком "плюс", а выражение 2x - 4 будет отрицательным и "выйдет" из под модуля со знаком "минус", получим уравнение:
- не входит в рассматриваемый промежуток и не является корнем уравнения.
3. При 
оба выражения 2x - 1 и 2x - 4 принимают положительные значения и "выйдут" из под модулей со знаками "плюс", получим уравнение:
- не входит в рассматриваемый промежуток и не является корнем уравнения.
Итак, уравнение имеет единственное решение, x = -3.
Ответ: x = -3.
3. Найти область определения функции:
Решение
1. Выражение, находящееся под знаком корня четной степени, должно быть неотрицательным, значит: 
2. Выражение под знаком логарифма должно быть строго положительным (область определения логарифмической функции - множество положительных действительных чисел): 
3. Знаменатель дроби не может быть равен нулю, значит: 
Получим систему неравенств:
Эта система неравенств равносильна совокупности двух систем:
(1) 
и (2) 
Решим каждую систему, используя числовые прямые (см. рис. 7):
(1) 
Рис. 7.
Решением системы является промежуток 
Решая вторую систему, выполним аналогичные преобразования и получим:
(2) 
Рис. 8
Эта система решений не имеет.
Ответ:
4. Решить уравнение:
Решение
Преобразуем уравнение: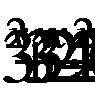 
Становится ясно, что мы имеем однородное показательное уравнение (показатели степеней всех одночленов в левой части уравнения равны 2x, а в правой части 0).
Такого вида уравнения решаются делением обеих его частей на одну из степеней с наибольшим показателем, в данном случае, на 
или на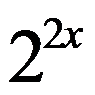 
. Это возможно, так как и 
, и 
при всех действительных значениях x.
Разделим обе части уравнения на 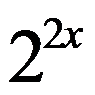, получим: 
Положим 
получим квадратное уравнение:
Значение 
не удовлетворяет условию 
и не может быть решением показательного уравнения.
Остается значение 
Проверка
При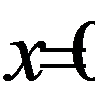 
получаем: 
