Найти асимптоты графиков следующих функций: 
14.1. 
;
14.2. 
;
14.3. 
;
14.4. 
;
14.5. 
;
14.6. 
;
14.7. 
;
14.8.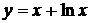 
;
14.9.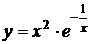 
;
14.10. 
;
14.11. 
;
14.12. 
.
Ответы
14.1. 
;
14.2. 
;
14.3.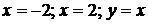 
;
14.4. 
;
14.5. 
;
14.6. 
;
14.7. 
;
14.8.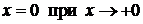 
;
14.9. 
;
14.10.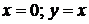 
;
14.11. 
;
14.12. 
.
Исследование функции и построение её графика
Если требуется построить график функции 
, то необходимо предварительно провести исследование её свойств. Это можно сделать по следующему плану:
1. Область определения функции 
.
2. Точки разрыва, поведение функции в окрестности точек разрыва.
3. Вертикальные асимптоты.
4. Точки пересечения графика функции с координатными осями.
5. Интервалы знакопостоянства функции.
6. Чётность, нечётность функции.
7. Периодичность функции.
8. Наклонные асимптоты графика функции.
9. Интервалы монотонности.
10. Экстремумы.
11. Интервалы выпуклости, вогнутости, точки перегиба.
12. Для более точного построения графика, можно найти значения функции в дополнительных точках.
Заметим, что приведённая схема исследования функций не является обязательной, этот порядок исследования может быть изменён в каждом конкретном случае.
Пример. Исследовать функцию 
и построить её график.
Решение.
1. Область определения функции 
.
2. 
– точка разрыва
3. Прямая 
является вертикальной асимптотой графика функции.
4. Точки пересечения графика функции с координатными осями:
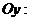
Отсюда видно, что график рассматриваемой функции пересекает обе координатные оси в начале координат, т.е. в точке 
.
5. Интервалы знакопостоянства функции:
а) 
б)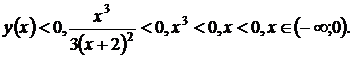 
6. Чётность, нечётность функции: рассматриваемая функция не является ни чётной, ни нечётной, поскольку её область определения не симметричная относительно нуля. К этому же выводу можно прийти, рассмотрев 
7. Рассматриваемая функция не является периодической.
8. Наклонная асимптота графика имеет уравнение 
где 
Следовательно, 
– наклонная асимптота при 
и при 
.
9. Интервалы монотонности найдём, исследуя производную функции:
Критические точки:
а) 
не существует при 
б) 
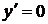при 
Отсюда видно, что функция возрастает при 
и при 
, убывает при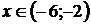 
.
10. Экстремумы:
Из п. 9 видим, что точкой максимума является 
вычислим
.
11. Интервалы выпуклости, вогнутости и точки перегиба найдём, исследуя производную второго порядка:
Критические точки II рода:
а) 
не существует при 
б) 
при 
Отсюда видно, что функция имеет выпуклый график на интервале 
и 
и вогнутый на интервале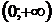 
.
Кроме того, график имеет точку перегиба, ее вторая координата 
, таким образом 
– точка перегиба.
Результаты проведенных исследований можно свести в таблицу:
| 
| 
| 
| 
|
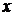
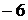
| 0 |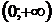
|
|
| + | 0 | – | не сущ. | + | 0 | + |
|
| – | – | – | не сущ. | – | 0 | + |
|
возрастает,
график
выпуклый
| 
|
убывает,
график
выпуклый
|  –вертикал.
асим-та
|
возрастает,
график
выпуклый
| 0 |
возрастает,
график
вогнутый
|
