4.1. 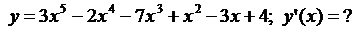
4.2. 
4.3. 
4.4. 
4.5. Найти 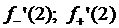 , если
, если 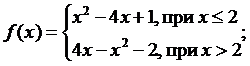
Сделать чертеж.
4.6. Найти 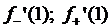 , если
, если 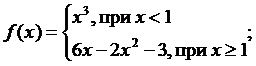
Сделать чертеж.
4.7. Найти  , если
, если 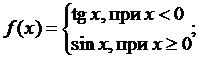
Сделать чертеж.
4.8. 
4.9. 
4.10. 
4.11. 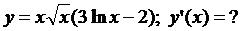
4.12. 
4.13. 
4.14. 
4.15. Тело массой 5 кг движется по прямой по закону  где t – время (с), s – путь (см). Вычислить кинетическую энергию
где t – время (с), s – путь (см). Вычислить кинетическую энергию  этого тела в конце 3-й секунды.
этого тела в конце 3-й секунды.
4.16. Дан закон прямолинейного движения точки:  , где t – время в секундах,
, где t – время в секундах,  . Найти скорость в конце 2-й и в конце 5-й секунды.
. Найти скорость в конце 2-й и в конце 5-й секунды.
4.17. Вывести формулу производной произведения трех дифференцируемых функций.
4.18. 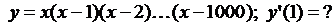
4.19. Под каким углом пересекаются кривые  и
и 
4.20. Составить уравнение той нормали к кривой  , которая перпендикулярна прямой
, которая перпендикулярна прямой  . Сделать чертеж.
. Сделать чертеж.
Ответы
4.1.  ;
;
4.2. 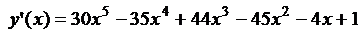
4.3. 
4.4. 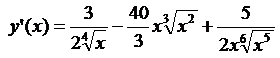
4.5. 
4.6. 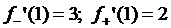
4.7. 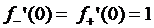
4.8. 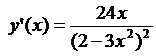
4.9. 
4.10. 
4.11. 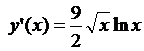
4.12. 
4.13. 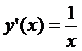
4.14. 
4.15. 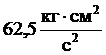
4.16. 
4.17. 
4.18. 
4.19. 
4.20. 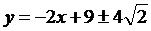
Производная сложной функции
Если функция  дифференцируема в точке
дифференцируема в точке  , а функция
, а функция 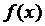 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке  , то сложная функция
, то сложная функция 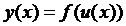 дифференцируема в точке
дифференцируема в точке  и ее производная вычисляется по формуле:
и ее производная вычисляется по формуле:
 .
.
Примеры с решениями
Пример 1. Найти производную функции  .
.
Решение. Обозначим 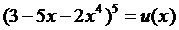 , тогда
, тогда  . По правилу дифференцирования сложной функции получаем
. По правилу дифференцирования сложной функции получаем

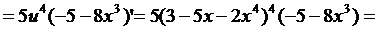

Ответ: 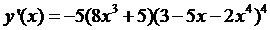 .
.
Пример 2. Найти производную функции  .
.
Решение. Здесь 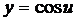 , где
, где 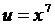

Ответ: 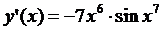
Пример 3. Найти производную функции 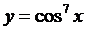 .
.
Решение. Здесь 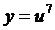 , где
, где 
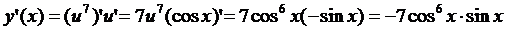
Ответ 
Пример 4. Найти производную функции 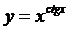 где
где 
Решение. Перед нами показательно-степенная функция, т.е. функция вида  .
.
Для ее дифференцирования можно воспользоваться несколькими способами. Один из них мы рассмотрим сейчас, другой будет разобран в параграфе о дифференцировании функций, заданных неявно. Итак, преобразуя заданную показательно-степенную функцию с помощью основного логарифмического тождества, приведем ее к виду показательной функции:
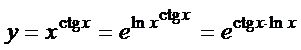
Получили сложную функцию 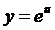 , где
, где 


Ответ: 
Примеры для самостоятельного решения
5.1. 
5.2. 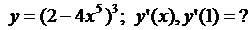
5.3. 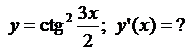
5.4. 
5.5. 
5.6. 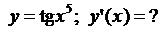
5.7. 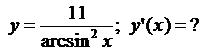
5.8. 
5.9. 
5.10. 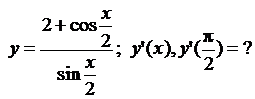
5.11. 
5.12. 
5.13. 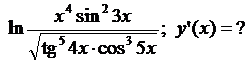
5.14. 
5.15. 
5.16. 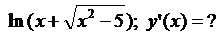
5.17. 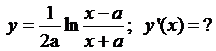
5.18. 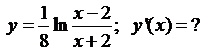
5.19. 
5.20. 
5.21. 
5.22. 
5.23. 
5.24. 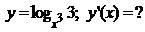
5.25. 
5.26. 
5.27. Составить уравнение той касательной к кривой  , которая перпендикулярна прямой
, которая перпендикулярна прямой 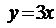 . Сделать чертеж.
. Сделать чертеж.
5.28. Зависимость между количеством  вещества, получаемого в некоторой химической реакции, временем t выражается уравнением:
вещества, получаемого в некоторой химической реакции, временем t выражается уравнением:  . Определить скорость реакции.
. Определить скорость реакции.
5.29. 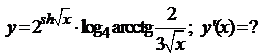
Ответы
5.1.  ; 5.2.
; 5.2.  ;
;
5.3. 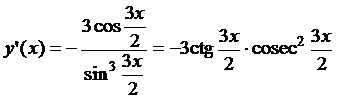 ;
;
5.4.  ;
;
5.5.  ;
;
5.6. 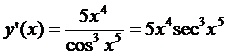 ; 5.7.
; 5.7.  ;
;
5.8.  ; 5.9.
; 5.9.  ;
;
5.10.  ;
;
5.11. 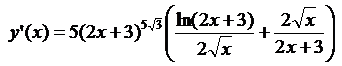 ;
;
5.12. 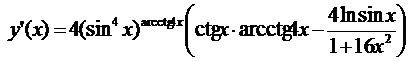 ;
;
5.13. 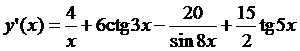 ;
;
5.14. 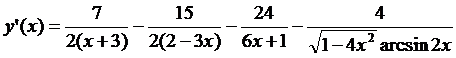 ;
;
5.15. 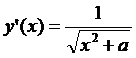 ; 5.16.
; 5.16.  ; 5.17.
; 5.17. 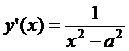 ;
;
5.18.  ; 5.19.
; 5.19. 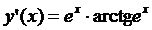 ; 5.20.
; 5.20. 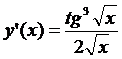 ;
;
5.21. 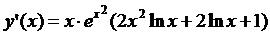 ; 5.22.
; 5.22.  ;
;
5.23.  ; 5.24.
; 5.24. 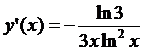 ; 5.25.
; 5.25. 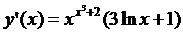 ;
;
5.26. 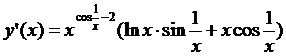 ; 5.27.
; 5.27.  ; 5.28.
; 5.28. 
5.29. 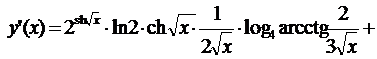

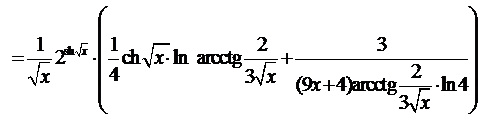 .
.
Дифференцирование функций, заданных неявно
Если у есть функция от х и при этом все соответствующие друг другу действительные значения х и у удовлетворяют уравнению 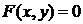 , то говорят, что функция y (x) задана уравнением
, то говорят, что функция y (x) задана уравнением 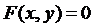 неявно. Для нахождения производной функции y (x), заданной неявно уравнением
неявно. Для нахождения производной функции y (x), заданной неявно уравнением  , достаточно продифференцировать по x обе части этого уравнения, рассматривая у как функцию от x, и из полученного уравнения выразить
, достаточно продифференцировать по x обе части этого уравнения, рассматривая у как функцию от x, и из полученного уравнения выразить  .
.
Примеры с решениями
Пример 1. Функция 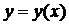 задана неявно уравнением
задана неявно уравнением 
Найти  .
.
Решение. Поскольку у является функцией от х, будем рассматривать y ³ как сложную функцию от х, следовательно,  . Продифференцировав по х обе части заданного уравнения, получим:
. Продифференцировав по х обе части заданного уравнения, получим:
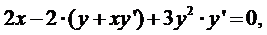
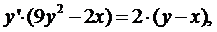

Ответ: 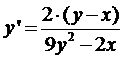 .
.
Пример 2. Найти производную функции  .
.
Решение. В данном примере при нахождении производной удобно от явного задания функции перейти к неявному. Прологарифмируем обе части равенства, задающего функцию (при этом обычно используют натуральный логарифм):
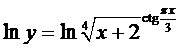
Используя свойства логарифмов, позволяющее показатель степени вынести множителем за знак логарифма, получим неявно заданную функцию у в форме,
удобной для дифференцирования:
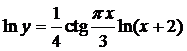
Продифференцируем по х обе части полученного уравнения.

Выразим y ′, домножив обе части этого уравнения на 

Ответ: 
Производную от логарифма функции называют логарифмической производной.
Пример 3. Найти производную функции
 .
.
Решение. Отметим, что данная функция на своей области определения 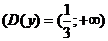 принимает положительные значения. Воспользуемся логарифмической производной и свойствами логарифмов:
принимает положительные значения. Воспользуемся логарифмической производной и свойствами логарифмов:


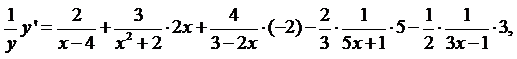
из этого равенства найдём 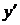 , умножив обе его части на
, умножив обе его части на
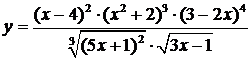 .
.

Ответ: 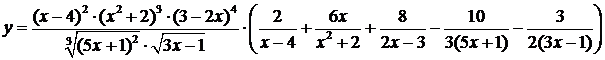 .
.
Пусть у есть функция от аргумента x:
 (1)
(1)
Задавая значения  , по формуле (1)будем получать соответствующие значения
, по формуле (1)будем получать соответствующие значения  . Можно, однако, считать у независимой переменной, а x – зависимой, задавать значения у и вычислять соответствующие им значения x. И если каждому значению у будет соответствовать единственное значение x, то равенство (1)можно рассматривать как неявное задание функции х от аргумента у. Такая функция называется обратной по отношению к данной функции у. Если уравнение (1)разрешить относительно х, получим явное выражение обратной функции, её обозначают
. Можно, однако, считать у независимой переменной, а x – зависимой, задавать значения у и вычислять соответствующие им значения x. И если каждому значению у будет соответствовать единственное значение x, то равенство (1)можно рассматривать как неявное задание функции х от аргумента у. Такая функция называется обратной по отношению к данной функции у. Если уравнение (1)разрешить относительно х, получим явное выражение обратной функции, её обозначают 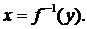
И для всех допустимых значений у будет выполняться равенство
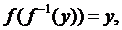 (2)
(2)
которое можно рассматривать как уравнение, задающее функцию  неявно.
неявно.
Для вычисления производной функции 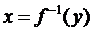 продифференцируем уравнение (2) по у:
продифференцируем уравнение (2) по у:

Откуда 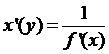 или
или 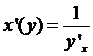 , если
, если 
Таким образом, для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной
данной функции.
Пример 4. Вывести формулу производной функции 
Решение. Рассмотрим функцию  , где
, где  ,
, 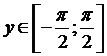 .
.
Обратная к ней функция имеет вид 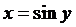 , причём
, причём  при
при 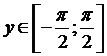 . Воспользовавшись правилом дифференцирования обратной функции, получим
. Воспользовавшись правилом дифференцирования обратной функции, получим

Поскольку cos y > 0 для всех 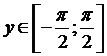 , то, учитывая, что
, то, учитывая, что  , получаем
, получаем 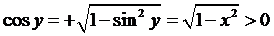 , при
, при 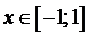 . Следовательно:
. Следовательно:
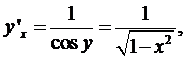
т.е.  , где
, где 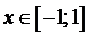
Ответ:  , где
, где 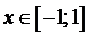 .
.
Пример 5. Вывести формулу производной функции, обратной к функции 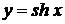 .
.
Решение. Дана функция 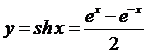 , её производная
, её производная  , для всех
, для всех 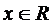 ,следовательно, функция
,следовательно, функция 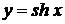 на всей действительной оси монотонно возрастает и имеет обратную функцию, обозначаемую
на всей действительной оси монотонно возрастает и имеет обратную функцию, обозначаемую  .
.
Уравнение 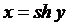 задаёт эту обратную функцию неявным образом. Продифференцируем обе части по х:
задаёт эту обратную функцию неявным образом. Продифференцируем обе части по х: 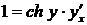 , откуда
, откуда  .
.
Из соотношения  выразим
выразим  , а поскольку
, а поскольку 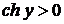 для всех
для всех 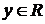 , то получим
, то получим 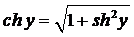 , где
, где  .
.
Таким образом, 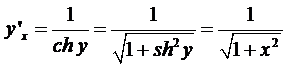 .
.
Итак, формула производной функции, обратной к гиперболическому синусу, имеет вид:
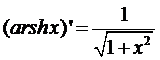
Ответ:  .
.






