Найти интервалы возрастания и убывания функций:
11.1. 
11.2. 
11.3. 
11.4. 
11.5. 
11.6. 
11.7.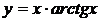 
11.8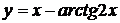 
11.9. 
11.10 
11.11. 
11.12. 
11.13. 
11.14. 
Найти экстремумы функций:
11.15.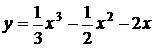 
11.16. 
11.17. 
11.18. 
11.19.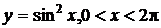 
11.20. 
11.21. 
Ответы
11.1. убывает при 
возрастает при 
;
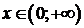11.2. возрастает при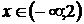 
и 
убывает при 
;
11.3. убывает при 
;
11.4. возрастает при 
и 
, убывает при 
и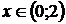 
;
11.5. возрастает при 
;
11.6. убывает при 
, возрастает при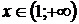 
;
11.7. убывает при возрастает при ;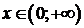
11.8. возрастает при 
и при 
, убывает при 
;
11.9. возрастает при 
, убывает при ;
11.10. убывает при 
и при 
, возрастает при 
;
11.11. возрастает при 
и при 
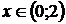, убывает при и 
;
11.12. убывает при и 
возрастает при 
;
11.13. возрастает при ;
11.14. убывает пр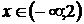и и ;
11.15. 
;
11.16. 
;
11.17.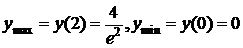 
;
11.18.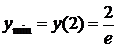 
;
11.19. 
;
11.20. 
;
11.21. 
Наименьшее и наибольшее значение функции, непрерывной на отрезке
Непрерывная на отрезке функция достигает на этом отрезке своих наибольшего и наименьшего значений (теорема Вейерштрасса). Эти значения функция может принимать либо в точках экстремума, находящихся внутри рассматриваемого отрезка, либо на концах этого отрезка. Поэтому решать задачу на наибольшее и наименьшее значения функции на отрезке можно, руководствуясь следующим правилом:
1) найти критические точки функции, принадлежащие интервалу 
;
2) вычислить значения функции в найденных критических точках и на концах отрезка 
;
3) из полученных значений выбрать наибольшее и наименьшее.
Замечание 1. Если функция имеет внутри отрезка лишь одну критическую точку, которая является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
Замечание 2. Если функция внутри отрезка не имеет критических точек, то это означает, что она строго монотонна на всем этом отрезке и своих наибольшего и наименьшего значений достигает в концах отрезка.
Примеры с решениями
Пример 1. Найти наименьшее и наибольшее значения функции 
на отрезке 
.
Решение. Находим 
. Отсюда видим, что критические точки: 
и 
. Находим значения функции в этих точках и на концах данного отрезка:
.
Из полученного следует, что 
− наименьшее, а 
− наибольшее значение функции на заданном отрезке.
Ответ: наименьшее значение 
, наибольшее значение .
Пример 2. Имеется смесь, состоящая из двух газов: оксида азота и кислорода. При какой концентрации кислорода содержащийся в смеси оксид азота окисляется с максимальной скоростью?
Решение. При наличии условий критической необратимости можно считать, что скорость реакции 
выражается формулой 
, где 
– концентрация 
в момент времени 
; 
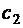– концентрация 
; 
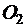– константа скорости, зависящая только от температуры. Выражая концентрации и 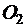в объёмных процентах, будем иметь 
, 
. Находим первую производную 
и, приравнивая её к нулю: 
. Найдём 
.
Найдем вторую производную: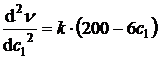 
, так как 
, то заключаем, что при 
скорость окисление имеет максимум. Далее, так как при , 
, то заключаем, что скорость окисления азота имеет максимум, если кислорода в газовой смеси содержится 33,3 %.
Ответ: При концентрации кислорода 33,3 %.
Пример 3. Требуется изготовить фильтр путём вырезания из круга радиуса 
сектора и свёртывания последнего в конус. При каком центральном угле сектора объём фильтра будет наибольшим?
Решение. Обозначим угол сектора через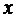 
, а радиус окружности основания конуса через 
. Тогда 
, откуда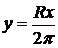 
. Если высота
фильтра 
, то объём его 
,
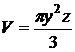где 
или 
.
Поэтому 
.
Итак, 
− функция от 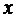, наибольшее значение которой на отрезке 
нужно найти. Находим первую производную и приравняем её к нулю:
, если 
, откуда, рассматривая только то решение, которое имеет смысл, находим 
.
По смыслу задачи ясно, что при фильтр будет иметь наибольший объём, равный:
Ответ: при фильтр будет иметь наибольший объём.
