Найти наибольшее и наименьшее значения функций на указанных отрезках:
12.1. 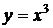 на отрезке
на отрезке  .
.
12.2. 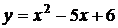 на отрезке
на отрезке  .
.
12.3.  на отрезке
на отрезке  и на отрезке
и на отрезке  .
.
12.4. 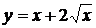 на отрезке
на отрезке  .
.
12.5.  на отрезке
на отрезке 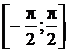 .
.
12.6. 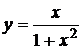 на отрезке
на отрезке 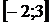 .
.
12.7.  на отрезке
на отрезке 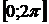 .
.
12.8. Какова должна быть сторона основания правильной треугольной призмы объёма  , чтобы её полная поверхность была наименьшей?
, чтобы её полная поверхность была наименьшей?
12.9.Каковы должны быть радиус основания и высота прямого кругового цилиндра объёма  , чтобы его полная поверхность была наименьшей?
, чтобы его полная поверхность была наименьшей?
12.10. Из квадратного жестяного листа, сторона которого 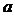 , желают сделать открытый сверху ящик наибольшего объёма, вырезая равные квадраты по углам, удаляя их и затем загибая. Какова должна быть длина сторон у вырезаемых квадратов?
, желают сделать открытый сверху ящик наибольшего объёма, вырезая равные квадраты по углам, удаляя их и затем загибая. Какова должна быть длина сторон у вырезаемых квадратов?
12.11. Из круга радиуса  вырезан сектор с центральным углом
вырезан сектор с центральным углом 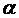 . Из этого сектора свёрнута коническая поверхность (прямой круговой конус). При каком
. Из этого сектора свёрнута коническая поверхность (прямой круговой конус). При каком 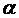 объём полученного конуса будет наибольшим?
объём полученного конуса будет наибольшим?
12.12. Разделить число 10 на такие две части, чтобы сумма их квадратов была наименьшей.
12.13. Найти высоту прямого кругового конуса с наибольшей боковой поверхностью, который можно вписать в данный шар радиуса  .
.
12.14. Найти высоту прямого кругового конуса с наименьшим объёмом описанного около шара радиуса  .
.
12.15. Найти измерения прямоугольника наибольшей площади, вписанного в эллипс  .
.
12.16. Принимая, что прочность бруска с прямоугольным поперечным сечением прямо пропорциональна ширине и кубу высоты, найти ширину бруска наибольшей прочности, который можно вырезать из бревна, диаметр которого равен 16 см.
12.17. Газ, содержащий оксид  , смешивается с воздухом. Определить, при каком содержании кислорода (%) в полученной смеси скорость окисления азота максимальна и какой объём добавленного к газу воздуха обеспечивает это количество кислорода в смеси?
, смешивается с воздухом. Определить, при каком содержании кислорода (%) в полученной смеси скорость окисления азота максимальна и какой объём добавленного к газу воздуха обеспечивает это количество кислорода в смеси?
12.18. Лампа висит над центром круглого стола радиуса  . При какой высоте лампы над столом освещённость предмета, лежащего на краю стола, будет наилучшая? (Освещённость прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника света).
. При какой высоте лампы над столом освещённость предмета, лежащего на краю стола, будет наилучшая? (Освещённость прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния от источника света).
12.19. Из круглого бревна диаметра  требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление:
требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление:
а) на сжатие;
б) на изгиб?
(Сопротивление балки на сжатие пропорционально площади её поперечного сечения, а на изгиб − произведению ширины этого сечения на квадрат его высоты).
12.20. Определить, при каком диаметре 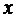 круглого отверстия в плотине секундный расход воды
круглого отверстия в плотине секундный расход воды 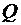 будет иметь наибольшее значение, если
будет иметь наибольшее значение, если
 ,
,
где  постоянная, равная глубине низшей точки отверстия, а
постоянная, равная глубине низшей точки отверстия, а  эмпирический коэффициент пропорциональности.
эмпирический коэффициент пропорциональности.
Ответы
12.1.  при
при  ;
;  при
при  ; 12.2.
; 12.2.  при
при  ;
;  при
при  ; 12.3. а)
; 12.3. а) 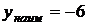 при
при  ;
;  при
при  , б)
, б) 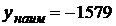 при
при  ;
;  при
при 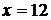 ; 12.4.
; 12.4.  при
при  ;
; 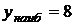 при
при  ; 12.5.
; 12.5.  при
при  ;
; 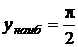 при
при  ; 12.6.
; 12.6.  при
при  ;
; 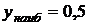 при
при  ; 12.7.
; 12.7.  при
при  ;
;  ; 12.8.
; 12.8.  ; 12.9. Высота цилиндра и диаметр основания равны; 12.10.
; 12.9. Высота цилиндра и диаметр основания равны; 12.10. 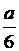 ; 12.11.
; 12.11.  ; 12.12. 5 и 5; 12.14.
; 12.12. 5 и 5; 12.14.  ; 12.15.
; 12.15.  ; 12.16. 8 см; 12.17. 7 %; 12.18.
; 12.16. 8 см; 12.17. 7 %; 12.18.  ; 12.19. а)
; 12.19. а)  и
и  ;б)
;б)  и
и  ; 12.20.
; 12.20.  .
.






