Определить вид кривой, заданной параметрически системой уравнений, и нарисовать её.
7.1. 
7.2. 
7.3. 
7.4. 
7.5. 
7.6. 
Найти производную функции y = y (x), заданной параметрически системой уравнений
7.7. 
7.8. 
7.9. 
7.10. 
7.11. 
7.12. 
7.13. Составить уравнения касательной и нормали к циклоиде  , проведенных в точке, для которой t =
, проведенных в точке, для которой t =  .
.
7.14. Составить уравнения касательной и нормали к астроиде  ,
,
проведенных в точке, для которой t =  .
.
7.15. Составить уравнения касательной и нормали к эллипсу  ,
,
проведенных в точке, для которой t =  . Сделать чертёж.
. Сделать чертёж.
7.16. Составить уравнения касательной и нормали к эллипсу  ,
,
проведенных в точке, для которой t =  . Сделать чертёж.
. Сделать чертёж.
7.17. Составить уравнения касательной и нормали к кривой, заданной параметрически системой уравнений  ,
,
проведенных в точке М0 (–1;1)
7.18. Составить уравнения касательной и нормали к кривой, заданной параметрически системой уравнений  ,
,
проведенных в точке М0 (1;–2)
Ответы
7.1. 3 x + 5 y – 11= 0 – уравнение прямой; 7.2. y = 7 x + 31 – уравнение прямой;
7.3.  – уравнение эллипса; 7.4.
– уравнение эллипса; 7.4.  – уравнение окружности; 7.5.
– уравнение окружности; 7.5.  – уравнение параболы; 7.6.
– уравнение параболы; 7.6.  –уравнение параболы; 7.7.
–уравнение параболы; 7.7.  ; 7.8.
; 7.8.  ;
;
7.9.  ; 7.10.
; 7.10.  ; 7.11.
; 7.11.  ;
;
7.12.  ; 7.13.
; 7.13.  ; 7.14. y =
; 7.14. y =  x +1, y = x;
x +1, y = x;
7.15. 7 x +5 y  35
35 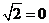 , 5 x
, 5 x  7 y +12
7 y +12 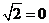 ; 7.16. 2
; 7.16. 2  x + y –8=0,
x + y –8=0,  x
x  6 y +9=0;
6 y +9=0;
7.17. y =  x, y = x + 2; 7.18. 5 x +3 y +1=0, 3 x
x, y = x + 2; 7.18. 5 x +3 y +1=0, 3 x  5 y
5 y  13=0.
13=0.
Дифференциал функции
Функция y = f (x) называется дифференцируемой в точке х 0 , если её приращение в этой точке, соответствующее приращению аргумента ∆ х, может быть представлено в виде
∆ y = A ·∆ x +α(∆ x)· ∆ x, (1)
где А – число, не зависящее от ∆ x (А зависит от х 0 ), α(∆ x) – бесконечно малая функция при ∆ x →0.
Дифференциалом этой функции в точке х 0 называется главная часть её приращения функции А ·∆ x (линейная относительно приращения аргумента). Для того чтобы функция y = f (x) была дифференцируемой в точке х 0, необходимо и достаточно, чтобы существовала конечная производная  ; при этом справедливо равенство
; при этом справедливо равенство  . Этот факт позволяет называть дифференцируемой всякую функцию, имеющую конечную производную. Выражение для дифференциала функции y = f (x) в точке х 0 имеет вид
. Этот факт позволяет называть дифференцируемой всякую функцию, имеющую конечную производную. Выражение для дифференциала функции y = f (x) в точке х 0 имеет вид
d y (х 0) = f '(х 0)· ∆ x. (2)
Для независимой переменной х её приращения совпадает с её дифференциалом: ∆ x = d x. Таким образом, для вычисления дифференциала функции используют формулу
d y = f '(х)· d x. (3)
Геометрически дифференциал функции y = f (x) в точке х 0 равен приращению ординаты касательной к графику этой функции в точке М 0(х 0; f (х 0)) при приращении аргумента ∆ x.

Основные свойства дифференциала
Если  ,
,  и
и  – дифференцируемые функции, то:
– дифференцируемые функции, то:
1. 
2. 
3. 
4. 
5. 
6. Cвойство инвариантности: дифференциал функции равен произведению производной этой функции на дифференциал аргумента, при этом безразлично, будет ли аргумент независимой переменной или дифференцируемой функцией от другой независимой переменной, т.е. если u = u (x) – функция, дифференцируемая в точке x, а y = f (u) – функция, дифференцируемая в соответствующей точке u, то

Таблица дифференциалов некоторых элементарных функций
Пусть u = u (x) – дифференцируемая функция, тогда
1. d (u α)=α· u α-1· du
2. d (au)= au · ln a · du
3. d (eu)= eu · du
4. 
5. 
6. 
7. 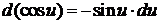
8. 
9. 
10. 
11. 
12. 
13. 
14. d (sh u) = ch u · du
15. d (ch u) = sh u · du
16. 
17. 
Если приращение аргумента ∆ х мало по абсолютной величине, то ∆ y ≈ d y, т.е. f (x 0+∆ x) – f (x 0) ≈ f '(x 0 )·∆ x, откуда получаем формулу для приближённых вычислений значения функции в точке:
f (x 0+∆ x) ≈ f (x 0) + f '(x 0 )·∆ x. (4)
Примеры с решениями
Пример 1. Найти дифференциал функции  .
.
Решение. Воспользуемся формулой (3).

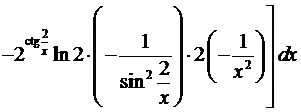
Ответ: 
Пример 2. Вычислить приближённо 1,986.
Решение. Рассмотрим число 1,986 как конкретное значение функции y = x6 в точке х 0+∆ х =1,98. Возьмём х 0=2, тогда ∆ х =–0,02. Вычислим f (x 0) = f (2) = 26=64. Найдем f '(x) = (x 6 )'=6 x 5 и вычислим f '(x 0) = f '(2)=6·25=6·32=192. Поставим полученные значения в формулу (4):
1,986 ≈ f (x 0)+ f '(x 0)·∆ x =64+192·(–0,02)=64–3,84=60,16.
Ответ: 1,986 ≈ 60,16.
Пример 3. Найти приближенно значение объёма V шара радиусом r =1,02 м.
Решение. Поскольку V (r) =  , то, полагая r 0 = 1, ∆ r = 0,02 и используя формулу (4), получаем:
, то, полагая r 0 = 1, ∆ r = 0,02 и используя формулу (4), получаем:
V (1,02) ≈ V (r 0)+ V '(r 0)·∆ r = V (1)+ V '(1)·0,02 =  +4π·0,02≈4,44.
+4π·0,02≈4,44.
Ответ: 4,44 м 3.






