График функции y = f (x)называется выпуклым вверх (выпуклым) на интервале (a; b) если в пределах этого интервала график функции y = f (x) лежит ниже любой своей касательной.
График функции y = f (x) называется выпуклым вниз (вогнутым) на интервале (a; b) если в пределах этого интервала график функции y = f (x) лежит выше любой своей касательной.
Точка графика функции y = f (x) M 0 (x 0; f (x 0))называется точкой перегиба графика, если при переходе x через x 0график меняет направление выпуклости.
Пусть функция y = f (x) дважды дифференцируема на интервале (a; b), тогда если в каждой точке этого интервала 
, то график функции на (a; b) выпуклый вверх (выпуклый), а если 
, то график функции на (a; b) выпуклый вниз (вогнутый). Это достаточные условия выпуклости (вогнутости) графика.
Если точка M 0 (x 0; f (x 0))является точкой перегиба графика функции y = f (x), то 
или 
не существует – необходимое условие точки перегиба.
Точка x 0 области определения функции, в которой вторая производная функции обращается в ноль или не существует, называется критической точкой II рода.
Для того чтобы точка M 0 (x 0; f (x 0))графика функции y = f (x) была точкой перегиба, достаточно, чтобы существовала конечная 
в некоторой окрестности точки x 0 (за исключением, может быть, самой точки x 0) и чтобы меняла знак при переходе x через x 0.
Пример 1. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции 
.
Решение.
Находим критические точки II рода:
а) 
не существует: 
,
б) 
при 
Вычислим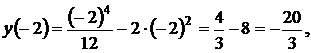 
Получим 
и 
− точки перегиба.
Ответ: 
– интервалы вогнутости, 
− интервал выпуклости, 
и 
− точки перегиба.
Пример 2. Найти интервал выпуклости, вогнутости и точки перегиба графика функции 
Решение.
Находим критические точки II рода:
а) 
не существует при 
,
б) 
:
Вычислим 
Получим 
− точка перегиба.
Ответ: 
− интервалы выпуклости, 
− интервал вогнутости, 
− точка перегиба.
Примеры для самостоятельного решения
Найти интервалы выпуклости, вогнутости и точки перегибы следующих функций:
13.1. 
;
13.2. 
;
13.3. 
;
13.4. 
;
13.5. 
;
13.6. 
;
13.7. 
;
13.8. 
;
13.9. 
;
13.10 
Ответы
13.1.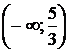 
− интервал выпуклости, 
− интервал вогнутости, 
− точка перегиба;
13.2. 
− интервал выпуклости, 
− интервал вогнутости,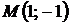 
− точка перегиба.
13.3. 
− интервалы выпуклости, 
− интервалы вогнутости, 
− точки перегиба.
13.4. 
− интервал выпуклости, 
− интервал вогнутости, точек перегиба нет.
13.5. 
− интервалы вогнутости, 
− интервал выпуклости, 
− точки перегиба.
13.6. 
− интервалы выпуклости, 
− интервалы вогнутости, 
− точки перегиба.
13.7. 
− интервал выпуклости, 
− интервал вогнутости, 
− точка перегиба.
13.8. − интервал вогнутости, − интервал выпуклости, 
− точка перегиба.
13.9. 
− интервалы вогнутости, 
− интервал выпуклости, 
− точка перегиба.
13.10. 
− интервалы вогнутости, − интервалы выпуклости, 
− точки перегиба.
Асимптоты графика функции
Прямая l называется асимптотой кривой y = f (x), если расстояние от точки M (x; y) кривой до прямой l стремится к нулю при неограниченном удалении этой точки по кривой от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности).
Прямая x = a является вертикальной асимптотой кривой y = f (x), если выполняется хотя бы одно из условий:
(1)
Прямая y = k x + b наклонная асимптота кривой y = f (x) при 
(при 
), если выполнены условия:
(2)
Частный случай наклонной асимптоты при 
– горизонтальная асимптота y = b.
Примеры с решениями
Пример 1. Найти асимптоты графика функции 
Решение. Область определения 
− точка разрыва графика функции, через нее может проходить вертикальная асимптота.
Рассмотрим 
, следовательно, и выполнено одно из условий (1) и прямая 
является вертикальной асимптотой.
Наклонная асимптота: y = k x + b, где k и b находим по формулам (2)
.
Получили k = 3 и b = 5, следовательно, наклонная асимптота имеет уравнение y = 3 x + 5.
Ответ: x = 2; y = 3 x + 5.
Пример 2. Найти асимптоты графика функции 
Решение. 
Область определения функции не имеет точек разрыва, следовательно, вертикальных асимптот нет.
Наклонная асимптота: y = k x + b, где k и b находим по формулам (2).
Получили k = 0 и b = 3, следовательно, прямая y = 3 является горизонтальной асимптотой графика рассматриваемой функции.
Ответ: y = 3.
Пример 3. Найти асимптоты графика функции 
Решение. 
вертикальных асимптот нет.
Наклонная асимптота: y = k x + b, где k и b находим по формулам (2).
, следовательно, при 
наклонной асимптоты нет.
Получили k = 0 и b = 0 при 
, это значит, что прямая y = 0 является горизонтальной асимптотой при .
Ответ: y = 0 (при ).
