8.1. Найти приращение ∆ y и дифференциал d y функции y = x 2 – 3 x + 2, соответствующие значению аргумента x 0=2 и двум различным приращениям аргумента (∆ x)1 =0,1 и (∆ x)2=0,01.
8.2. Найти приращение ∆ y и дифференциал d y функции y = x 3 – 2 x –5, соответствующие значению аргумента х 0 = –3 и приращениям аргумента (∆ x)1=0,1 и (∆ x)2 =0,01.
8.3. Доказать, что для линейной функции y = kx + b приращение ∆ y и дифференциал d y совпадают.
8.4. Вычислить приближённое значение площади круга, радиус которого равен 3,02 м.
8.5. Вычислить приближённое значение arcsin 0,51.
8.6. Вычислить приближённое значение arctg 0,98.
8.7. Вычислить приближённое значение 
.
8.8. Вычислить приближённое значение 
.
8.9. 
8.10. 
8.11. 
8.12. 
8.13. 
8.14. 
8.15. 
8.16.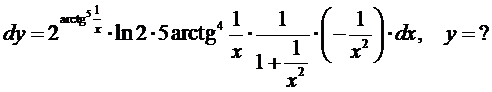 
Ответы
8.1. 1) при ∆ x = 0,1; ∆ y = 0,11; d y = 0,1; 2) при ∆ x = 0,01; ∆ y = 0,0101; d y = 0,01;
8.2. 1) при ∆ x = 0,1; ∆ y = 2,411; d y = 2,5; 2) при ∆ x = 0,01; ∆ y = 0,249101, d y = 0,25.; 8.4. 28,66 м2; 8.5. 0,513; 8.6. 0,775; 8.7. 1,007; 8.8. 1,999;
8.9.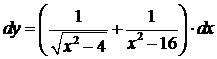 
;
8.10. 
;
8.11. 
; 8.12. 
; 8.13. 
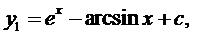
; 8.14. 
; 8.15. 
; 8.16. 
.
Производные и дифференциалы высших порядков
Производная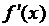 
от функции 
называется производной первого порядка или первой производной и представляет собой некоторую функцию, которая также может иметь производную. Тогда производная от производной первого порядка называется производной второго порядка или второй производной. Ее обозначают одним из следующих символов:
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка или третьей производной. Аналогично определяются производные четвертого, пятого и т.д. порядков. Вообще, производной n -го порядка от функции 
называется производная от производной (n – 1)-го порядка:
Производные высших порядков вычисляются последовательным дифференцированием функции.
Если функция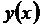 
задана параметрически системой уравнений: 
, где 
и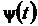 
− дифференцируемые функции и 
, то для нахождения производных функции 
можно использовать следующие формулы:
и т.д.
Производную второго порядка можно также вычислить по формуле:
Для нахождения второй производной от функции, заданной неявно, равенство 
задающее ее первую производную, дифференцируют по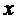 
(рассматривая 
как функцию от 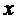), а затем в правой части полученного равенства на место 
подставляют задающее ее выражение 
. Аналогично поступают при нахождении производных более высоких порядков.
Дифференциалом второго порядка функции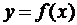 
называется дифференциал от дифференциала первого порядка этой функции:
Аналогично определяется дифференциал третьего порядка:
Вообще, 
.
Есл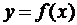и и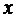 
– независимая переменная, то дифференциалы высших порядков вычисляются по формулам:
_________
Свойством инвариантости дифференциалы высших порядков (начиная со второго) не обладают.
Примеры с решениями
Пример 1. Найти 
от функции 
Решение.
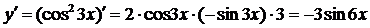
Ответ: 
Пример 2. Найти производную n -го порядка от функции 
Решение. Определяем последовательно 
Мы установили закон, по которому строятся последовательные производные от 
. Теперь можно дать и общую формулу для n -й производной от этой функции. Действительно,
______________________________
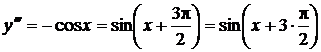
Ответ: 
Пример 3. Найти производную третьего порядка от функции 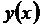, заданной параметрически уравнениями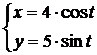 
Решение.
Ответ: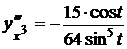 
Пример 4. Найти производную n -го порядка от функции 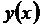, если она задана параметрически уравнениями 
Решение.
и т.д.
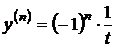
Ответ: 
Пример 5. Найти производную второго порядка от функции 
, заданной неявно уравнением 
Решение. Найдем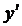 
, продифференцировав по 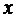обе части уравнения, задающего неявно функцию , рассматривая при этом 
как функцию от .
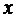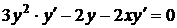
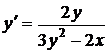
Теперь продифференцируем по 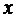обе части полученного равенства (рассматривая 
как функцию от ).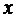
И теперь в полученное выражение подставим 
:
Ответ: 
Пример 6. Найти дифференциал 22-го порядка функции 
Решение.
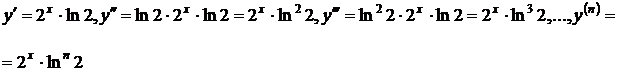
Следовательно, 
тогда 
Ответ: 
