Функция  называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале  , если она определена на этом интервале (
, если она определена на этом интервале ( ) и если для любых двух точек
) и если для любых двух точек  и
и 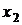 , принадлежащих этому интервалу, из условия
, принадлежащих этому интервалу, из условия  следует неравенство
следует неравенство 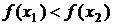 (
( ).
).
Функция  называется неубывающей (невозрастающей) на интервале
называется неубывающей (невозрастающей) на интервале  , если она определена на этом интервале (
, если она определена на этом интервале ( ) и если для любых двух точек
) и если для любых двух точек  и
и 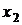 , принадлежащих этому интервалу, из условия
, принадлежащих этому интервалу, из условия  следует неравенство
следует неравенство  (
( ).
).
Функция  называется монотонной на интервале
называется монотонной на интервале  , если она является неубывающей на этом интервале или невозрастающей на этом интервале. Если функция
, если она является неубывающей на этом интервале или невозрастающей на этом интервале. Если функция  возрастающая на
возрастающая на  или убывающая на
или убывающая на  , то ее называют строго монотонной на интервале
, то ее называют строго монотонной на интервале  .
.
Если функция  дифференцируема и является возрастающей (убывающей) в некотором промежутке, то
дифференцируема и является возрастающей (убывающей) в некотором промежутке, то 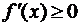 (
( ) для любого
) для любого 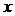 из этого промежутка. При этом точки, в которых
из этого промежутка. При этом точки, в которых  не заполняют никакого отрезка (необходимое условие возрастания (убывания) дифференцируемой функции в промежутке).
не заполняют никакого отрезка (необходимое условие возрастания (убывания) дифференцируемой функции в промежутке).
Если функция  дифференцируема и является неубывающей (невозрастающей) в некотором промежутке, то
дифференцируема и является неубывающей (невозрастающей) в некотором промежутке, то  (
(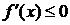 ) для любого
) для любого 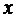 из этого промежутка – необходимое условие неубывания (невозрастания) дифференцируемой функции в промежутке.
из этого промежутка – необходимое условие неубывания (невозрастания) дифференцируемой функции в промежутке.
Если в любой точке 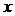 некоторого промежутка
некоторого промежутка  (
( ), то в этом промежутке функция
), то в этом промежутке функция  возрастает (убывает) − достаточное условие возрастания (убывания) дифференцируемой функции в промежутке.
возрастает (убывает) − достаточное условие возрастания (убывания) дифференцируемой функции в промежутке.
Рассмотрим функцию  , непрерывную в точке
, непрерывную в точке  . Точка
. Точка  называется точкой максимума функции
называется точкой максимума функции  , если существует такая окрестность точки
, если существует такая окрестность точки  , что для все
, что для все 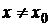 из этой окрестности
из этой окрестности  . Значение функции в точке максимума называется максимумом функции:
. Значение функции в точке максимума называется максимумом функции:  .
.
Точка  называется точкой минимума функции
называется точкой минимума функции  , если существует такая окрестность точки
, если существует такая окрестность точки  , что для всех
, что для всех  из этой окрестности
из этой окрестности 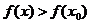 . Значение функции в точке минимума называется минимумом функции:
. Значение функции в точке минимума называется минимумом функции: 
Точки максимума и минимума функции называются точками экстремума функции. Значения функции в точках экстремума называются экстремумами функции.
Если функция  имеет в точке
имеет в точке  экстремум, то
экстремум, то 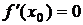 или
или  не существует – необходимое условие экстремума. Отсюда следует, что точки экстремума функции следует искать только среди тех точек, в которых производная функции равна нулю или не существует, такие точки называются критическими или стационарными точками функции.
не существует – необходимое условие экстремума. Отсюда следует, что точки экстремума функции следует искать только среди тех точек, в которых производная функции равна нулю или не существует, такие точки называются критическими или стационарными точками функции.
Если функция  непрерывна в некоторой окрестности критической точки
непрерывна в некоторой окрестности критической точки  и дифференцируема в этой окрестности (за исключением может быть, самой точки
и дифференцируема в этой окрестности (за исключением может быть, самой точки  ) и если при переходе
) и если при переходе 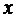 через
через  (слева направо):
(слева направо):
1)  меняет знак с «+» на «−», то
меняет знак с «+» на «−», то  – точка максимума функции,
– точка максимума функции,
2)  меняет знак с «−» на «+», то
меняет знак с «−» на «+», то  – точка минимума функции,
– точка минимума функции,
3)  не меняет знак, то в точке
не меняет знак, то в точке  функция не имеет экстремума.
функция не имеет экстремума.
Если в критической точке  функция
функция  дважды дифференцируема, то определить характер экстремума (если в точке
дважды дифференцируема, то определить характер экстремума (если в точке  функции имеет экстремум) можно по знаку второй производной, а именно:
функции имеет экстремум) можно по знаку второй производной, а именно:
1) если  , то
, то  − точка максимума функции,
− точка максимума функции,
2) если  , то
, то  − точка минимума функции.
− точка минимума функции.
Примеры с решениями
Пример 1. Найти интервалы возрастания и убывания функции 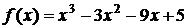 .
.
Решение. Область определения функции  . Находим производную
. Находим производную 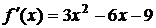 . Для нахождения интервалов возрастания функции решаем неравенство
. Для нахождения интервалов возрастания функции решаем неравенство  ,
,  ,
,  , получаем
, получаем  , на этих интервалах функция возрастает. Для нахождения интервалов убывания решаем неравенство
, на этих интервалах функция возрастает. Для нахождения интервалов убывания решаем неравенство  ,
,  ,
,  , получаем
, получаем  , на этом интервале функция убывает.
, на этом интервале функция убывает.
Можно поступить и так: находим точки, в которых  ,
,  ,
, 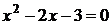 ,
,  . Эти точки отметим на числовой прямой и определим знаки производной на образовавшихся интервалах:
. Эти точки отметим на числовой прямой и определим знаки производной на образовавшихся интервалах:

Интервалы, на которых производная функции имеет знак «+», являются интервалами возрастания функции, а те, на которых «−» − интервалами убывания.
Ответ: функция возрастает на интервале 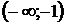 и
и  ; функция убывает на интервале
; функция убывает на интервале 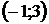
Пример 2. Найти интервалы монотонности функции 
Решение. Область определения функции  . Находим производную
. Находим производную  , решаем уравнение
, решаем уравнение  ,
,
 .
.
Изображаем область определения функции и наносим на нее точку  , после чего определяем знак производной на каждом из образовавшихся интервалов:
, после чего определяем знак производной на каждом из образовавшихся интервалов:

Теперь видим, что на интервале  функция убывает, а на интервале
функция убывает, а на интервале  возрастает.
возрастает.
Ответ: функция возрастает на интервале  , убывает на интервале
, убывает на интервале 
Пример 3. Найти экстремумы функции 
Решение. Область определения функции  . Находим производную
. Находим производную  . Находим критические точки:
. Находим критические точки:  не существует при
не существует при  ,
,  при
при  .
.
Изображаем область определения функции (это вся числовая прямая) и наносим на нее критические точки, после чего определяем знак производной на каждом из образовавшихся интервалов:

По знаку производной на каждом интервале определяем характер монотонности функции и видим точки экстремума. Остается вычислить сами экстремумы функции:  .
.
Ответ: 
Пример 4. Найти экстремумы функции 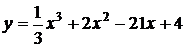 .
.
Решение.



Критические точки: 


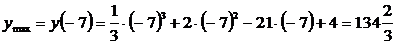
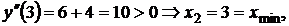
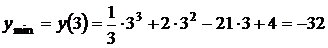
Ответ:  ,
,  .
.






