ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
(ПРИМЕРЫ И ЗАДАЧИ)
Утверждено Редакционным советом
университета в качестве учебного пособия
Москва
2013
УДК 517 (075)
ББК 22.161.1
Д50
Авторы: Е. Г. Рудаковская, О. В. Аверина, C. М. Воронов, Т. Н. Старшова, Т. В. Хлынова, Т. В. Ригер
Рецензенты:
Доктор физико-математических наук, профессор Российского химико-технологического университета имени Д. И. Менделеева
В. М. Аристов
Доктор технических наук, профессор Российского химико-технологического университета имени Д. И. Менделеева
Л. С. Гордеев
Дифференциальное и интегральное исчисление функции одной пере-
Д50 менной (примеры и задачи): учеб. пособие / Е. Г. Рудаковская, О. В.
Аверина, С. М. Воронов, Т. Н. Старшова, Т. В. Хлынова, Т. В. Ригер; под
ред. Е. Г. Рудаковской. – М.: РХТУ им. Д. И. Менделеева, 2013. – 132 с.
ISBN 978-5-7237-1114-3
Пособие представляет курс практических занятий по математическому анализу, проводимых кафедрой высшей математики РХТУ им. Д. И. Менделеева.
Охватывает следующие разделы курса математического анализа: теория пределов, дифференциальное исчисление функций одной переменной, интегральное исчисление функций одной переменной. В каждом параграфе изложены теоретические основы, необходимые для решения практических задач, примеры с подобранным решением, задачи для самостоятельного решения с ответами. Большое внимание уделено разбору примеров по изучаемым темам, имеющим прикладное значение для других дисциплин.
Предназначено для студентов I курса всех факультетов и колледжей РХТУ им. Д. И. Менделеева.
УДК 517 (075)
ББК 22.161.1
ISBN 978-5-7237-1114-3 © Российский химико-технологический
университет им. Д. И. Менделеева, 2013
Оглавление
Глава 1. Дифференциальное исчисление функции одной переменной….………4
§1. Предел функции. Вычисление предела функции с помощью алгебраических преобразований…………………………………………………………..……….4
§2. Вычисление предела функции с использованием замечательных пределов………………………………………………………………………....10
§3. Производная функции одной переменной (определение, геометрический смысл)…………………………………………………..………………………..13
§4. Дифференцирование по формулам, правила дифференцирования ……………………………………………………………..………………..……19
§5. Производная сложной функции………………………………………..….23
§6. Дифференцирование функций, заданных неявно…………………..…….27
§7. Дифференцирование функций, заданных параметрически………….…..33
§8. Дифференциал функции……………………………………………..…….37
§9. Производные и дифференциалы высших порядков…………………..….42
§10. Раскрытие неопределённостей. Правило Лопиталя……………..………49
§11. Возрастание и убывание функции. Экстремумы функции…………..…56
§12. Наименьшее и наибольшее значение функции, непрерывной
на отрезке……………………………………………………………………......61
§13. Направление выпуклости графика функции. Точки перегиба………...65
§14. Асимптоты графика функции………………………………………….…68
§15. Исследование функции и построение её графика…………………..…...71
Глава 2. Интегральное исчисление функции одной переменной.................…..79
§1. Первообразная функция и неопределенный интеграл......................…….79
§2. Интегрирование посредством разложения подынтегральной функции на слагаемые…………………………………………………………….………85
§3. Интегрирование подстановкой …………………………………….……...87
§4. Интегрирование по частям……………………………………..…………..90
§5. Интегрирование рациональных дробей………………………………..….96
§6. Интегрирование тригонометрических выражений…………………..….102
§7. Интегрирование некоторых видов иррациональных выражений….…...107
§8. Определённый интеграл……………………..…………………………....112
§9. Приложения определенного интеграла……………………..……….......118
§10. Несобственные интегралы…………………………..……………….......126
ГЛАВА 1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Предел функции. Вычисление предела функции с помощью алгебраических преобразований
Пусть функция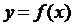 
определена в некоторой окрестности точке 
, кроме, быть может, самой точки .
Определение 1. Число A называется пределом (по Коши) функции 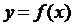в точке (или при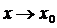 
), если для любого числа 
> 0 найдётся отвечающее ему положительное число d такое, что для всех значений, удовлетворяющих условию 
, справедливо неравенство: 
. При этом записывают:
(или 
при 
).
Примеры с решениями
Пример 1. Используя определения, доказать, что функция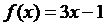 
в точке 
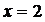имеет предел, равный 5, т.е. 
.
Решение. Возьмём любое >0. Задача состоит в том, чтобы для этого найти такое d > 0, при котором из неравенства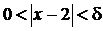 
следовало бы неравенство 
. Преобразуя последнее неравенство, получаем 
, или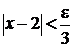 
. Отсюда видно, если взять 
, то для всех 
, удовлетворяющих неравенству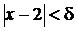 
, выполняется требуемое неравенство 
. Это и означает, что 
.
