Рассмотрим на примере.
Пример 6. Вычислить предел:
Решение. Имеем неопределённость вида 
. Домножим числитель и знаменатель дроби, предел которой мы ищем, на выражение 
, сопряжённое числителю.
Ответ: 
.
Для пределов подобного вида способ домножения на сопряжённое выражение является типичным.
3. Случай неопределённости вида 
Для раскрытия исходной неопределённости нужно разделить числитель и знаменатель дроби на переменную x в наибольшей степени, которая входит в данную дробь, учитывая, что величина обратная бесконечно большой есть бесконечно малая величина.
Пример 7. Вычислить предел:
Решение. Имеем неопределённость вида . Разделим числитель и знаменатель дроби на 
.
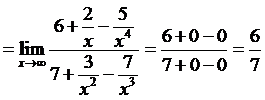
Ответ: 
.
В общем случае можно использовать правило:
4. Случай неопределённостей вида: 
Эти неопределённости сводятся к неопределённостям вида 
одним из следующих способов:
а) приведение дробей к общему знаменателю,
б) преобразование функции к виду дроби,
в) избавление от иррациональности (домножение на сопряжённое выражение числителя и знаменателя дроби).
Пример 8. Вычислить предел:
Решение.
Ответ: 2.
Примеры для самостоятельного решения
Вычислить пределы:
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
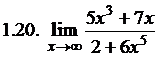
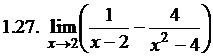
Ответы
1.1. 
. 1.2. – 2. 1.3. 14. 1.4. 1. 1.5. 
. 1.6. –9. 1.7. 3. 1.8. 
. 1.9. 
. 1.10. 6.
1.11. 
. 1.12. 
1.13. 
1.14. . 1.15. 
. 1.16. 
. 1.17. 
. 1.18. 
. 1.19. ∞. 1.20. 0. 1.21. 1. 1.22. 
. 1.23.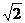 
. 1.24. ∞. 1.25. . 1.26. 2. 1.27. . 1.28. 0. 1.29. 0. 1.30. 2. 1.31. 0. 1.32. 1,5. 1.33. –∞. 1.34. +∞. 1.35. +∞. 1.36. +∞. 1.37. –∞. 1.38. –∞.
Вычисление предела функции с использованием замечательных пределов
Первым замечательным пределом называется предел вида:
.
Примеры с решениями
Пример 1. Вычислить предел:
Решение. 
Ответ: a.
Пример 2. Вычислить предел:
Решение. Используем тригонометрические формулы:
Ответ: 4.
Вторым замечательным пределом называется предел вида:
Пример 3. Вычислить предел:
Ответ: 
.
Пример 4. Вычислить предел:
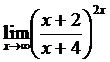
Решение. 
Ответ: 
.
Примеры для самостоятельного решения
Вычислить пределы:
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
|
|
| 
|
| 
|
| 
|
| 
|
| 
|
| 
|
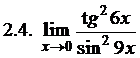
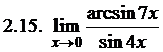
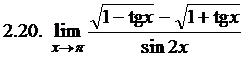
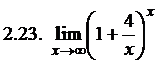
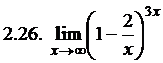
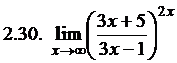
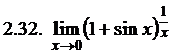
Ответы
2.1. 5. 2.2. 3. 2.3. 
. 2.4. 
2.5. – 4,5. 2.6. – 
. 2.7. 0,5. 2.8. 2. 2.9. – . 2.10. 5. 2.11. 3. 2.12. 0. 2.13. cos 3. 2.14. 1. 2.15. 1,75. 2.16. 
. 2.17. – 
. 2.18. 14.
2.19. – 1. 2.20. – 0,5. 2.21. . 2.22. – 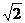. 2.23. 
. 2.24. 
. 2.25. 
. 2.26. 
. 2.27.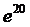 
. 2.28. 
. 2.29. 
. 2.30. . 2.31. 0. 2.32. 
. 2.33. 1. 2.34. –7.
Производная функции одной переменной
(определение, геометрический смысл)
Рассмотрим функцию 
, определенную в точке x и в некоторой окрестности этой точки.
Определение 1. Производной функции в точке x называется предел отношения приращения функции в точке x к приращению аргумента при условии стремления приращения аргумента к нулю, если такой предел существует:
(1)
Для обозначения производной используют символы: 
Определение 2. Односторонние пределы 
называются соответственно левой производной и правой производной функции в точке x (если эти пределы существуют). Их обозначают 
. Для существования производной функции в точке x необходимо, чтобы ее правая и левая производные в этой точке существовали и были равны:
Примеры с решениями
Пример 1. Найти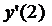 
для функции 
пользуясь определением производной.
Решение. Пусть 
– приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:
Воспользуемся определением производной:
Ответ: 
Пример 2. Найти 
для функции 
в точке х = 0.
Решение. Пусть – приращение аргумента. Найдем соответствующее ему приращение функции в точке x = 0:
Воспользуемся определением:
Ответ: 
.
Заметим, что функция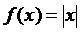 
не имеет производной в точке x = 0, так как 
С геометрической точки зрения значение производной функции в точке x 0 представляет собой угловой коэффициент касательной, проведенной к графику функции в точке M 0 (x 0; f (x 0)), т.е. 
, где 
– угол наклона касательной к оси О x.
Уравнение касательной, проведенной к графику функции в точке с абсциссой x 0, имеет вид:
. (2)
Уравнение нормали к графику той же функции в точке с абсциссой x 0:
(3)
если 
.
Если в точке x 0 функция имеет бесконечную производную, т.е. 
или 
или 
, то касательная к графику этой функции в точке с абсциссой x 0 перпендикулярна оси 
Уравнение касательной в этих случаях имеет вид: x = x 0 , а уравнение нормали – 
. Если же 
, то уравнение нормали: x = x 0 .
Углом между кривыми 
и 
называется угол между касательными, проведёнными к этим кривым в точке их пересечения 
(4)
если 
.
Если же 
, то касательные перпендикулярны и 
.
Пример 3. Составить уравнения касательной и нормали к графику функции 
в точке с абсциссой x 0 = 2.
Решение. Воспользуемся уравнениями касательной (2) и нормали (3).
В эти уравнения надо поставить x 0 = 2; 
и найденное в примере 1 значение 
. Получим уравнение касательной: 
и уравнение нормали:
Ответ: 
– уравнение касательной;
– уравнение нормали.
Пример 4. Пользуясь определением, найти значение производной функции 
в точках 
Решение. Выведем формулу производной функции в любой точке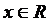 
, пользуясь определением. Зададим аргументу приращение 
и найдем соответствующее ему приращение функции:
Итак, 
. Вычислим значения производной в указанных точках:
Ответ: 
Если при прямолинейном движении точки задан закон движения 
то скорость движения v в момент времени t 0 есть производная по времени: 
, а ускорение а в момент времени t 0 определяется производной скорости движения по времени: 
