Теорема 7.12. Размерность пространства решений однородной СЛУ равна
n-rgA.
Доказательство. Рассмотрим однородную систему линейных уравнений Ax=0. Множество решений системы не изменится, если из матрицы удалить линейно зависимые строки. Поэтому, можно считать, что число строк матрицы A совпадает с её рангом. Пусть J – множество номеров столбцов матрицы A, в которых расположен максимальный не нулевой минор, T – остальное множество номеров столбцов. Систему уравнений можно записать в виде 
, где 
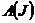подматрица матрицы A расположенная в столбцах с номерами из J, 
- вектор, образованный компонентами x с номерами из J. Обозначим столбец, у которого все компоненты равны 0, кроме i-ой, равной 1, через 
. Вектор 
, 
является решением системы линейных уравнений. Обозначим этот вектор через 
(
). Система векторов 
является линейно независимой, так как в строках с номерами из T расположена единичная матрица, определитель которой не равен 0. Пусть y - произвольное решение системы линейных уравнений, тогда 
, и, учитывая равенство 
выводим 
и, значит, 
. Поскольку произвольное решение системы линейных уравнений является линейной комбинацией линейно независимой системы векторов , то эта система векторов является базисом и размерность подпространства решений равна n-rgA.
Позднее будет показано, что любое подпространство может быть задано некоторой СЛУ.
Теорема 7.13 Общее решение неоднородной системы линейных уравнений равно сумме частного решения и общего решения соответствующей однородной системы линейных уравнений.
Доказательство. Очевидно.
Множество решений системы линейных уравнений (не однородной) называется линейным многообразием.
Двойственное пространство
Пусть V – линейное пространство над полем P. Линейной формой (функцией) над V называется функция, удовлетворяющая условиям
Свойство 7.3 Линейная форма определена своими значениями на базисных векторах.
Доказательство. Пусть 
базис V. Вектор x из V разложим по базису 
. Тогда 
.
На множестве линейных форм определим операции сложения 
и умножения на скаляр 
.
Свойство 7.4 Множество линейных форм образует линейное пространство
Доказательство. Проверим все аксиомы векторного пространства.
Определение 7.14 Пространство линейных форм называется двойственным к исходному пространству.
Свойство 7.5 Двойственное пространство изоморфно исходному.
Доказательство. Для доказательства достаточно показать совпадение размерностей исходного и двойственного пространств. Пусть базис V. Определим линейные формы 
. Эти линейные формы линейно независимы, и через них выражается любая другая линейная форма. Таким образом, эти линейные формы образуют базис двойственного пространства, и размерность двойственного пространства совпадает с размерностью исходного пространства.
Элементы двойственного пространства называются ковекторами.
Подпространству W линейного пространства V поставим в соответствие подпространство 
двойственного пространства, состоящее из линейных форм, обращающихся в ноль на всех векторах из W. Отметим некоторые свойства этого соответствия.
Свойство 7.6. Справедливы равенства
1. 
2. 
3. 
4. 
Доказательство. Поскольку только нулевая форма обращается в ноль на всех векторах из V, то первое равенство установлено.
Пусть 
, тогда линейная форма f равна 0 на всех векторах из U+W, а, значит, 
и 
. Тем самым установлено включение 
. Пусть 
, тогда линейная форма f равна 0 на всех векторах из U и W, а, значит, она равна 0 на всех векторах из U+W, то есть . Таким образом, получено включение 
. Объединив включение получим второе равенство.
Третье равенство доказывается аналогично второму равенству.
Пусть 
базис W, дополним его до базиса всего пространства векторами 
. Определим линейные формы 
, где j=1,…,n. Линейные формы 
образуют базис двойственного пространства и 
принадлежат . Покажем, что базис . Возьмём произвольную линейную форму f из и разложим её по базису 
. Тогда 
, и, значит, 
. Тем самым четвёртое равенство доказано.
Из четвёртого свойства вытекает, что размерность пространства решений системы однородных линейных уравнений равна разности размерности всего пространства и (строчечного) ранга матрицы.
Вектор из пространства V можно рассматривать как линейную форму в двойственном пространстве. Действительно, и . Следовательно, подпространству F двойственного пространства к V можно поставить в соответствие подпространство 
пространства V, образованное векторами из V, обращающими в 0 все линейные формы из F.
Свойство 7.7 Пусть 
- подпространство конечномерного линейного пространства 
. Тогда 
.
Доказательство. Пусть 
, тогда 
для всех линейных форм из , а, значит, 
. Тем самым установлено включение 
. Далее, 
, следовательно, .
Следствие 7.12 Любое подпространство арифметического пространства можно задать системой линейных уравнений.
Доказательство. Очевидным образом следует из равенства .
Рассмотрим задачу построения системы однородных линейных уравнений задающих линейную оболочку системы векторов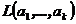 
(для определённости будем считать эту систему векторов линейно независимой а исходное пространство арифметическим). Следуя проведённым теоретическим построениям, мы должны поступать следующим образом. Дополним систему векторов 
до базиса всего пространства векторами 
. Далее, найдём обратную матрицу к матрице A, составленную из векторов 
. Последние n-k строк матрицы 
будут определять требуемую систему. Однако, можно уменьшить объём вычислений. Действительно, базис подпространства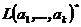 
определяется как базис пространства решений однородной системы линейных уравнений 
.
Следствие 7.13 Любое линейное многообразие можно задать системой неоднородных уравнений.
