Изоморфизм линейных пространств.

Определение 7.13 Линейные пространства над числовым полем P называются изоморфными, если существует взаимно однозначное соответствие между векторами этих пространств, сохраняющее операции сложения векторов и умножения на скаляр.

Для доказательства изоморфизма линейных пространств V и W требуется построить взаимно однозначное отображение , обладающее свойствами сохранения операции:

1. ,

2. ,

Следствие 7.10. При изоморфизме нулевой вектор переходит в нулевой вектор.

Доказательство. Действительно, .

Лемма 7.3 Пусть V, W, U линейные пространства над полем P. Пусть W изоморфно V, а V изоморфно U, тогда W изоморфно U.

Доказательство. По условию существуют взаимно однозначные соответствия  и , обладающие свойствами сохранения операции, то есть

1. ,

2. ,

3. ,

4. ,

Отображение , получаемое последовательным применением  и , является взаимно однозначным соответствием между пространством W и пространством U. Далее, имеем

1. , где .

2. , .

Тем самым изоморфизм установлен.

Лемма 7.4 Пространство V над числовым полем P размерности n изоморфно арифметическому пространству .

Доказательство. Пусть  - базис V. Каждому вектору x из V поставим в соответствие его координаты. Данное соответствие является взаимно однозначным (Теорема 7.4) и сохраняет операции. Тем самым изоморфизм установлен.

Лемма 7.5. При изоморфизме базис переходит в базис.

Доказательство. Пусть  - изоморфизм пространства V на W,  - базис V. Разложим произвольный вектор x из V по базису . По определению изоморфизма , и значит, в силу взаимно однозначности отображения, через систему векторов  линейно выражается любой вектор пространства W. Методом от противного покажем линейную независимость системы векторов . Пусть не так, тогда найдутся числа , не все равные нулю, что 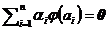. Последнее равенство, используя свойства изоморфизма, запишем в виде . В силу взаимно однозначности изоморфизма выводим , т.е. система векторов  - линейно зависима. К полученному противоречию с условиями нас привело допущение о линейной зависимости системы векторов . Таким образом, система векторов  является полной линейно независимой системой, т.е. базисом линейного пространства W.

Теорема 7.10. Линейные пространства V и W над полем P изоморфны тогда и только тогда, когда их размерности равны.

Доказательство. Если размерности пространств V и W совпадают и равны n, то оба пространства изоморфны (Лемма 7.4), а, значит и между собой (Лемма 7.3). Обратно, если пространства изоморфны, то при изоморфизме базис переходит в базис (Лемма 7.5), и, значит, размерности пространств равны.

Изоморфизм пространств позволяет переносить терминологию, принятую в одном пространстве на изоморфные пространства. Например, можно говорить о прямой в пространстве многочленов.

Задание прямой и плоскости в пространстве. Деление отрезка. Задачи.

Опишем множество точек, лежащих на прямой l, проходящей через точки A, B. Если , то векторы  и  коллинеарные, т.е отличаются числовым множителем. Пусть 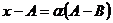. Выразим отсюда x: 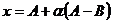. Данное уравнение называется параметрическим уравнением прямой. Вектор A-B принадлежит прямой и называется направляющим вектором прямой.

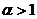В зависимости от параметра  получаем различные точки прямой. Если , то получим точку X из отрезка , причём . Если , то получаем точку X, что отрезок  содержит точку A, причём . Если , то получаем точку X, что отрезок  содержит точку B, причём .

Пусть A,B,C три точки не лежащие на одной прямой. Опишем множество точек плоскости , проходящей через эти три точки. Точка x лежит на плоскости тогда и только тогда, когда вектор x-A является линейной комбинацией векторов B-A и C-A. Следовательно, параметрическое уравнение плоскости имеет вид 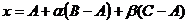. Векторы B-A и C-A называются направляющими векторами плоскости.

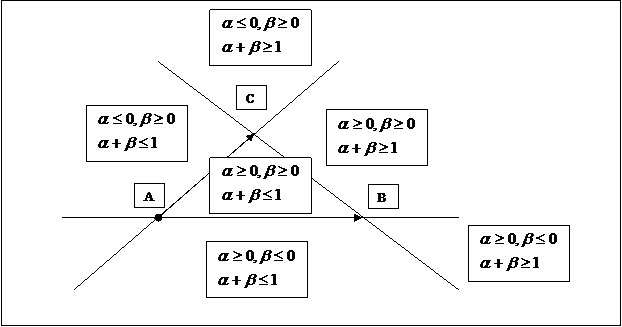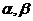В зависимости от значений параметров  получаются точки из разных областей. На рисунке приведено разбиение на области и указаны значения параметров.

Пусть система векторов 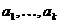 - линейно не зависима. Множество точек вида  называется линейным многообразием.

Для иллюстрации приведённой теории решим следующую задачу:

Доказать, что в произвольном тетраэдре, все отрезки соединяющие вершины с точкой пересечения медиан треугольника, образованного вершинами противоположной грани, пересекаются в одной точке и найти отношение, в котором делит эти отрезки точка пересечения.

В начале решим вспомогательную задачу: выразить точку пересечения медиан треугольника через его вершины. Обозначим вершины треугольника через A,B,C. Векторы AB и AC выберем в качестве базиса. Тогда, точки имеют координаты A=(0,0), B=(1,0), C=(0,1). Обозначим середину отрезка [BC] через F. Точка F имеет координаты (1/2,1/2). Отрезок [AF] делится точкой пересечения медиан O в соотношении 2:1, следовательно, O=(1/3,1/3). Таким образом, . Рассматривая плоскость как линейное многообразие, получаем . Обозначим через ABCD вершины тетраэдра. В качестве базиса выберем векторы AB, AC, AD. Тогда A=(0,0,0), B=(1,0,0), C=(0,1,0), D=(0,0,1). Точку пересечения медиан треугольника BCD обозначим через F, треугольника ACD – через G. Координаты этих точек равны F=(1/3,1/3,1/3), G=(0,1/3,1/3). Параметрическое уравнение прямой AF имеет вид x=a(1/3,1/3,1/3), а прямой BG x=(1,0,0)+b(-1,1/3,1/3). Точка пересечения H этих прямых находится из системы уравнений a(1/3,1/3,1/3)=(1,0,0)+b(-1,1/3,1/3) и H=(1/4,1/4,1/4) (получается при a=b=3/4). Отрезки AF и BG в точке пересечения делятся в отношении 3:1. Выбирая в качестве B любую вершину тетраэдра (отличную от A) получим, что все отрезки соединяющие вершины с точкой пересечения медиан треугольника, образованного вершинами противоположной грани, пересекаются в одной точке H и делятся в отношении 3:1.

 

Ранги матрицы.

Для матрицы можно дать три определения ранга:

1. Столбцовый ранг - ранг системы столбцов.

2. Строчечный ранг - ранг системы строк.

3. Минорный ранг - Порядок наибольшего (по размеру) отличного от нуля минора.

Теорема 7.11. Все ранги равны.

Доказательство. Для доказательства достаточно показать равенство столбцового и минорного рангов. Действительно, при транспонировании матрицы минорный ранг не меняется, а столбцовый ранг становится строчечным.

Первое доказательство. Воспользуемся критерием линейной независимости (Теорема 7.9).

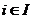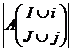Второе доказательство. Пусть максимальный по порядку не нулевой минор расположен на пересечении строк с номерами  и столбцов с номерами из . Система линейных уравнений , где  является крамеровской и, значит, имеет единственное решение, которое равно . Для  выполняется равенство , при s=1,…,n. Пусть , . Рассмотрим минор . Вычтем из последнего столбца остальные столбцы с коэффициентами  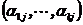и разложим по последнему столбцу. В результате получим  (все миноры порядка больше k равны 0). Поскольку , то равенство  выполняется при . Таким образом, все столбцы линейно выражаются через столбцы с номерами из множества . Система уравнений  имеет единственное нулевое решение, следовательно, столбцы матрицы A с номерами из J образуют базу. Ранг системы столбцов совпадает с порядком максимального не нулевого минора, что и требовалось доказать.

Следствие 7.11. Ранг произведения матриц не превосходит ранга сомножителей.

Доказательство. Пусть C=AB. По определению произведения матриц, строки матрицы C являются линейными комбинациями строк матрицы B и, значит, 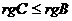. Аналогично, столбцы матрицы C – линейные комбинации столбцов матрицы A, и .