Элементарные преобразования матрицы A, такие как подстановка строк; прибавление к одной строке другой строки, умноженной на число; умножение строки на число можно трактовать как умножение матрицы A слева на некоторую матрицу, соответствующую элементарному преобразованию. Выпишем некоторые такие матрицы с описанием элементарных преобразований.
1. Подстановка строк i и j эквивалентна умножению слева на матрицу, которая получается из единичной матрицы подстановкой i и j строк.
2. Умножение строки i на число a эквивалентно умножению слева на матрицу, отличающейся от единичной только одним элементом, стоящим на пересечении i строки и столбца и равного a.
3. Прибавление к i-ой строке j-ой, умноженной на число a равно сильно умножению слева матрицу, отличающейся от единичной только элементом, стоящим на пересечении i-ой строки и j-го столбца и равного a.
Аналогично, преобразования над столбцами матрицы эквивалентны умножению справа на матрицы элементарных преобразований.
Построение обратной матрицы
Пусть A невырожденная матрица. Рассмотрим задачу построения обратной матрицы. Припишем справа к матрице A единичную матрицу. Элементарными преобразованиями строк добьемся, что бы на месте матрицы A располагалась единичная матрица. С точки зрения матричных операций получим равенство  , где
, где  матрицы элементарных преобразований. Положим
матрицы элементарных преобразований. Положим  . Равенство
. Равенство  равносильно равенствам
равносильно равенствам  и
и 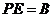 . Из этих равенств делаем вывод, что B – обратная матрицы к матрице A.
. Из этих равенств делаем вывод, что B – обратная матрицы к матрице A.
Совершенно аналогично, если припишем единичную матрицу снизу к матрице A, а затем элементарными преобразованиями столбцов добьемся чтобы на месте матрицы A стояла единичная матрица, то на месте единичной матрицы будет стоять обратная к A матрица.
Блочные матрицы
Напомним, матрица – таблица чисел. Часто полезно рассматривать матрицу как таблицу, элементами которой являются не числа, а матрицы меньших порядков. При такой точке зрения говорят о блочном строении матрицы. Использование блочного строения матриц позволяет строить более эффективные алгоритмы.
Теорема 6.3. Умножение блочных матриц.
Пусть матрица A имеет блочное строение  , а матрица B имеет блочное строение
, а матрица B имеет блочное строение  , причем размеры блоков согласованы так, что существует произведение
, причем размеры блоков согласованы так, что существует произведение 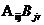 при любых i,j,r. Тогда произведение матриц C=AB будет иметь блочное строение
при любых i,j,r. Тогда произведение матриц C=AB будет иметь блочное строение  , причем
, причем  . Последнее выражение имеет такой же вид, как если бы умножали матрицы с числовыми элементами.
. Последнее выражение имеет такой же вид, как если бы умножали матрицы с числовыми элементами.
Доказательство. Элемент блочной матрицы A, расположенный в блоке  на пересечении строки r и столбца s обозначим через
на пересечении строки r и столбца s обозначим через 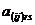 . По определению произведения матриц, имеем
. По определению произведения матриц, имеем  , где
, где  - количество столбцов в блоке
- количество столбцов в блоке  (по условиям теоремы это число совпадает с количеством строк блока
(по условиям теоремы это число совпадает с количеством строк блока  ). Сумма
). Сумма  является элементом матрицы
является элементом матрицы  , расположенным на пересечении строки r и столбца s. Следовательно,
, расположенным на пересечении строки r и столбца s. Следовательно, 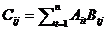 , что и требовалось доказать.
, что и требовалось доказать.
Использования блочного представления матриц позволяет получать более эффективные алгоритмы для решения задач линейной алгебры.
Алгоритм Штрассена
Использование правил блочного произведения матриц позволяет уменьшить общее количество операций, а значит, и время выполнения работы программы. Допустим, требуется умножить квадратные матрицы A и B порядка 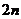 . При перемножении матриц, по формулам, приведённым в определении произведения, потребуется
. При перемножении матриц, по формулам, приведённым в определении произведения, потребуется  умножений и сложений. Разобьём матрицы A и B на блоки
умножений и сложений. Разобьём матрицы A и B на блоки 
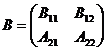 порядка n. Вычисление произведения блочных матриц проведём по формулам Штрассена
порядка n. Вычисление произведения блочных матриц проведём по формулам Штрассена
-
 потребуется
потребуется  умножений и сложений
умножений и сложений -
 потребуется
потребуется  умножений и сложений
умножений и сложений -
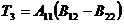 потребуется
потребуется  умножений и сложений
умножений и сложений -
 потребуется
потребуется  умножений и сложений
умножений и сложений -
 потребуется
потребуется  умножений и сложений
умножений и сложений -
 потребуется
потребуется  умножений и сложений
умножений и сложений -
 потребуется
потребуется  умножений и сложений
умножений и сложений -
 потребуется
потребуется 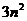 сложений
сложений -
 потребуется
потребуется  сложений
сложений -
 потребуется
потребуется  сложений
сложений -
 потребуется
потребуется 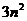 сложений.
сложений.
Всего, для вычисления произведения матриц по формулам Штрассена, потребуется  операций сложения и умножения. При выполнении неравенства
операций сложения и умножения. При выполнении неравенства  (n>7) формулы Штрассена приводят к меньшему объёму вычислений. Выигрыш в числе операций будет увеличиваться, если при вычислении произведения матриц (шаги1-7) использовать ту же схему.
(n>7) формулы Штрассена приводят к меньшему объёму вычислений. Выигрыш в числе операций будет увеличиваться, если при вычислении произведения матриц (шаги1-7) использовать ту же схему.
Обозначим через  число операций сложения и умножения, используемых при умножении матриц n -го порядка по формулам Штрассена. Справедлива рекуррентная формула
число операций сложения и умножения, используемых при умножении матриц n -го порядка по формулам Штрассена. Справедлива рекуррентная формула  . Положим
. Положим  . Тогда
. Тогда 
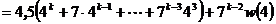 , далее, свернём сумму по формуле суммы членов геометрической прогрессии и заметим
, далее, свернём сумму по формуле суммы членов геометрической прогрессии и заметим  . В результате получим
. В результате получим  . Подставив вместо k его выражение через n (
. Подставив вместо k его выражение через n ( ) получим
) получим  (
( ).
).
Кронекерово произведение
Определение 6.3Пусть  и
и  - прямоугольные матрицы соответственно размеров
- прямоугольные матрицы соответственно размеров  и
и  . Кронекеровым произведением
. Кронекеровым произведением  называется матрица
называется матрица  размеров
размеров  следующего блочного строения
следующего блочного строения  .
.
Приведем основные свойства кронекерова произведения матриц.
Свойство 6.2. Пусть  и
и  , тогда
, тогда  .
.
Доказательство следует из правила блочного произведения матриц.
Свойство 6.3. Пусть существуют  и
и  , тогда
, тогда  .
.
Доказательство. По доказанному ранее (Свойство 6.2), имеем  . Из полученного равенства вытекает требуемое утверждение.
. Из полученного равенства вытекает требуемое утверждение.
Свойство 6.4.  .
.
Доказательство следует из определения операций кронекерова произведения и транспонирования матриц.
Свойство 6.5. Пусть  - квадратная матрица порядка
- квадратная матрица порядка 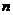 , а
, а  - квадратная матрица порядка
- квадратная матрица порядка  , тогда
, тогда  .
.
Доказательство. Если матрица A имеет верхний треугольный вид, то утверждение получается последовательным разложением определителя по теореме Лапласа по первым m столбцам. Если матрица A имеет нижний треугольный вид, то утверждение получается последовательным разложением определителя по теореме Лапласа по первым m строкам. Рассмотрим случай, когда матрица A не треугольная. Элементарными преобразованиями со строками (а именно, подстановкой строк и прибавлением к одной строки, другой строки умноженной на число) приведём матрицу A к треугольному виду T. Тогда  , где
, где  - матрица элементарных преобразований. Имеет место равенство
- матрица элементарных преобразований. Имеет место равенство  , из которого выводим
, из которого выводим  . Поскольку T – треугольная матрица, то
. Поскольку T – треугольная матрица, то  . Матрица элементарного преобразования
. Матрица элементарного преобразования  , если она соответствует прибавлению к некоторой строке другой строки, умноженной на число, имеет треугольный вид, и, значит
, если она соответствует прибавлению к некоторой строке другой строки, умноженной на число, имеет треугольный вид, и, значит  . Если матрица элементарного преобразования
. Если матрица элементарного преобразования  соответствует подстановке двух строк, то
соответствует подстановке двух строк, то  . Таким образом,
. Таким образом,  . Для доказательства утверждения осталось заметить равенство
. Для доказательства утверждения осталось заметить равенство  .
.
Следствие 6.2.  .
.
Доказательство проведём индукцией по n. Положим  и
и  . При n=2 имеем
. При n=2 имеем  , т.е. утверждение верно. Пусть оно справедливо при n-1. Тогда
, т.е. утверждение верно. Пусть оно справедливо при n-1. Тогда  , что и требовалось доказать.
, что и требовалось доказать.
Формула Фробениуса
Пусть матрица A имеет блочный вид  . Припишем к ней справа единичную матрицу и найдём обратную к матрице A. Для этого выполним следующие действия:
. Припишем к ней справа единичную матрицу и найдём обратную к матрице A. Для этого выполним следующие действия:
- Умножим (слева) на матрицу
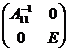 (конечно в предположении существования обратной матрицы). В результате получим матрицу
(конечно в предположении существования обратной матрицы). В результате получим матрицу  .
. - Вычтем из второй блочной строки первую, умноженную на матрицу
 (на языке матриц мы умножим слева на матрицу
(на языке матриц мы умножим слева на матрицу  ). В результате получится матрица
). В результате получится матрица  .
. - Умножим слева на матрицу
 . В результате получим матрицу
. В результате получим матрицу 
- Вычтем из первой блочной строки вторую, умноженную на матрицу
 (т.е. умножим слева на матрицу
(т.е. умножим слева на матрицу  ). В результате получится матрица
). В результате получится матрица 
Тем самым найдена обратная матрица к матрице A. Формула  называется формулой Фробениуса. Использование формулы Фробениуса позволяет уменьшить количество арифметических операций при вычислении обратной матрицы.
называется формулой Фробениуса. Использование формулы Фробениуса позволяет уменьшить количество арифметических операций при вычислении обратной матрицы.
Обозначим через 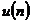 и
и  число арифметических операций необходимых, соответственно, для обращения и умножения матриц n-го порядка. Имеет место рекуррентная формула
число арифметических операций необходимых, соответственно, для обращения и умножения матриц n-го порядка. Имеет место рекуррентная формула  . Положим
. Положим  , тогда при умножении матриц по формулам Штрассена
, тогда при умножении матриц по формулам Штрассена  . Применив формулу k раз (учитывая
. Применив формулу k раз (учитывая  ) получим
) получим  . Подставив вместо k его выражение через n (
. Подставив вместо k его выражение через n ( ) получим
) получим 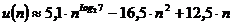 .
.
Линейные пространства.
Определение 7.1Множество V называется линейным пространством над числовым полем P, если определены две операции
1. сложения элементов из V (+)
2. умножения элемента из V на элемент из P (*)
Эти операции удовлетворяют аксиомам:
1. ассоциативность сложения, т.е.  (x+ y)+ z= x+(y+ z)
(x+ y)+ z= x+(y+ z)
2. коммутативность сложения, т.е.  x+ y= y+ x
x+ y= y+ x
3. существование 0, т.е.  x+0=x
x+0=x
4. существование обратного  x+ y=0, обратный обозначают – x.
x+ y=0, обратный обозначают – x.
5. ассоциативность умножения 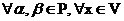
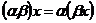 .
.
6. Дистрибутивность 
7. Дистрибутивность 
8. умножение на 0 0 x=0. (в правой части 0 – элемент из V)
9. умножение на 1; 1x=x
Элементы линейного пространства называются векторами, а элементы числового поля P – скалярами.
Примеры линейных пространств.
1. Множество непрерывных функций над R
2. Множество векторов пространства над R
3. Арифметическое пространство (множество наборов из n чисел из P) 
Определение 7.2Подмножество W линейного пространства V над полем P называется подпространством, если оно является пространством (в смысле выполняются все аксиомы)
Теорема 7.1. Для того, что бы подмножество W линейного пространства V над числовым полем P являлось подпространством необходимо и достаточно выполнения двух условий:
1. 
2. 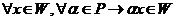
Примеры подпространств:
1. Множество многочленов образует подпространство в пространстве всех функций.
2. Множество решений системы линейных уравнений Ax=0 в арифметическом пространстве
3. Плоскость, прямая в пространстве векторов.
4. Линейная оболочка системы векторов (то есть множество всех линейных комбинаций векторов) 
Следствие 7.1. Пересечение линейных подпространств является подпространством
Доказательство заключается в проверке выполнений условий Теорема 7.1.
Определение 7.3 Суммой подпространств V+W называется множество векторов вида 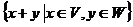
Следствие 7.2 Сумма подпространств – подпространство.
Доказательство заключается в проверке выполнений условий Теорема 7.1.
Следствие 7.3 Сумма подпространств V+W – наименьшее подпространство, которое содержит как V так и W.
Доказательство. Обозначим через F подпространство, являющееся пересечением всех подпространств содержащих подпространства V и W. Так как V+W содержит оба этих подпространства, то  . Поскольку F содержит как V так и W, и является подпространством (Следствие 7.1), то сумма векторов x+y, где
. Поскольку F содержит как V так и W, и является подпространством (Следствие 7.1), то сумма векторов x+y, где  и
и  , принадлежит F. Таким образом, установлено включение
, принадлежит F. Таким образом, установлено включение  . Объединяя включения, получаем равенство V+W=F.
. Объединяя включения, получаем равенство V+W=F.






