Преобразованиями, описанными в разделе 5.1, приводим определитель к треугольному виду. Далее, определитель равен произведению диагональных элементов.
Приведём пример вычисления определителя матрицы 
. Вычтем из каждой строки предыдущую (начиная с последней строки). В результате получим треугольную матрицу, по диагонали которой стоят 1. Определитель равен 1.
Определитель Вандермонда
Пусть даны числа 
. Матрицей Вандермонда называется матрица, у которой на пересечении i-го столбца и j-ой строки расположен элемент, равный 
. Обозначим через 
матрицу Вандермонда. Определитель матрицы Вандермонда является многочленом от , т.к.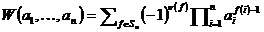 
. Рассмотрим определитель как многочлен от 
. Степень этого многочлена равна n-1, а его корни равны 
(т.к. определитель матрицы с двумя одинаковыми строками равен нулю). Следовательно, 
, где q – коэффициент при старшей степени. Легко убедиться, что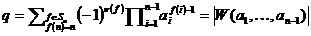 
. Таким образом получена рекуррентная формула 
, последовательным применением которой придём к равенству 
.
Теорема Лапласа
Определение 5.2. Пусть 
и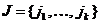 
множества номеров строк и столбцов матрицы A, соответственно. Подматрицу матрицы A, расположенную на пересечении строк с номерами из I и столбцов с номерами из J, обозначим как 
, а подматрицу, получаемую из A, вычеркиванием строк с номерами из I и столбцов с номерами из J обозначим через 
. Определитель называется минором, а определитель - дополнительным минором.
Лемма 5.1 Справедливо равенство 
.
Доказательство. Выразим правую часть равенства через элементы исходной матрицы. Для этого заметим, что 
и 
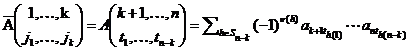, где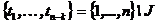 
(номера 
упорядочены в порядке возрастания). Подставим данные выражения в правую часть и перемножим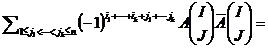 
Первая сумма состоит из 
слагаемых, вторая сумма – из k! слагаемых и третья сумма – (n-k)! слагаемых. Следовательно, общее количество слагаемых равно n!. Покажем, что каждое из этих слагаемых входит в определитель с тем же самым знаком. Слагаемое имеет вид 
, где 
. В определителе оно соответствует подстановке 
. Представим подстановку 
в виде произведения трёх подстановок 
, где 
, 
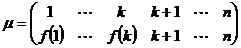и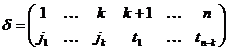 
. Легко убедиться в справедливости равенств 
, 
, 
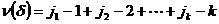. Следовательно, 
, и таким образом, совпадение знаков показано, что завершает доказательство леммы.
Теорема 5.1 (Лапласа). Пусть множество номеров строк. Справедливо равенство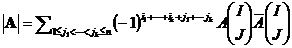 
.
Доказательство. Обозначим через B матрицу, получающуюся из матрицы A последовательной подстановкой строк с номерами из I на место первых k строк (при этом порядок остальных строк не нарушается). Для этого потребуется 
подстановок строк, и значит,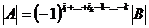 
. Разложив определитель матрицы B (Лемма 5.1), и заметив, что 
, 
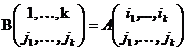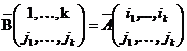выводим .
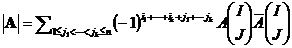Следствие 5.1. Пусть 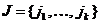множество номеров столбцов. Справедливо равенство 
.
Вытекает из теоремы Лапласа и равенства определителей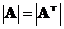 
.
Следствие 5.2. (разложение по столбцу). Пусть j – номер столбца. Справедливо равенство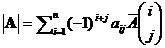 
.
Следствие 5.3 (разложение по строке) Пусть i – номер строки. Справедливо равенство 
.
Примеры использования теоремы Лапласа.
Умножение матриц
Определение 5.3. Пусть A матрица размерами m*n, а B матрица размерами n*k. Произведением матриц A*B называется матрица C размерами m*k, элементы которой находятся по формулам 
. Другими словами, элемент матрицы произведения, расположенный на пересечении i-ой строки и j-го столбца равен произведению i-ой строки A на j-ый столбец B.
Свойство 5.7 Пусть A*B=C. Строка i матрицы C является комбинацией строк матрицы B, причём коэффициенты берутся из i строки матрицы A. Столбец j матрицы C является комбинацией столбцов матрицы A, причём коэффициенты берутся из j столбца матрицы B.
Свойство 5.8. Произведение матриц не коммутативно.
Свойство 5.9. Произведение матриц ассоциативно.
Формула Бине-Кощи
Теорема 5.2 (Бине-Коши).. Пусть A матрица размерами m*n, а B матрица размерами n*m (n больше либо равно n). Справедливо равенство 
, где 
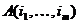- матрица, образованная столбцами матрицы A с номерами 
, а 
- матрица, образованная строками матрицы B с номерами .
Доказательство. Пусть C=AB. По определению определителя 
. Выразим элементы C через элементы A и B, получим 
. Перемножим все суммы придем к выражению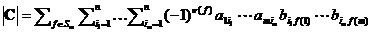 
. Поменяем порядок суммирования, поставив сумму по подстановкам на последнее место. Вынесем за знак суммы сомножители не зависящие от f получим 
. Сумма 
есть определитель матрицы , следовательно, 
. Определитель, содержащий одинаковые строки равен 0, поэтому исключив из последней суммы слагаемые с одинаковыми номерами строк, придем к выражению 
. Для упорядочивания строк матрицы 
потребуется 
подстановок соседних строк (см.Теорема 4.1), следовательно, 
и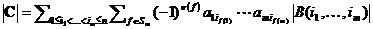 
. Вынесем за знак последней суммы множители не зависящие от f 
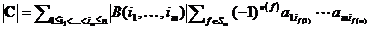. Сумма 
есть определитель матрицы 
, следовательно,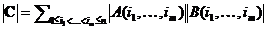 
, что и требовалось.
Следствие 5.4. Пусть A и B квадратные матрицы порядка n. Тогда определитель произведения равен произведению определителей 
.
Операции с матрицами
Обратная матрица
Квадратная матрица n-го порядка, у которой по диагонали 1, а все остальные элементы 0, называется единичной и обозначается E.
Для любой матрицы A справедливы равенства AE=EA=A. Таким образом, единичная матрица играет роль 1 среди матриц.
Определение 6.1. Матрица B называется обратной к матрице A, если AB=BA=E. Обратная матрица обозначается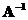 
.
Понятие обратной матрицы существует только для квадратных матриц.
Свойство 6.1. Если обратная матрица существует, то она единственна.
Доказательство проведем методом от противного. Пусть существует две обратные матрицы к A, которые обозначим через B и C. Рассмотрим произведение BAC. С одной стороны (BA)C=EC=C, а с другой B(AC)=BE=B. Результат не зависит от способа расстановок скобок, поэтому B=C.
Определение 6.2. Матрица называется невырожденной, если ее определитель отличен от 0.
Теорема 6.1. Необходимым и достаточным условием существования обратной матрицы к A является ее невырожденность.
Доказательство. Пусть к матрице A существует обратная 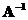. Из равенства 
следует равенство определителей 
, откуда 
.
Пусть . Построим матрицу B, элементы которой равны 
. Найдем AB. Элемент матрицы произведения, стоящий на пересечение строки i и столбца j равен 
. Сумма 
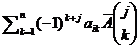является разложением по строке j определителя матрицы, отличающейся от матрицы A только строкой j, вместо которой стоит строка i. Если 
, то эта матрица имеет две одинаковые строки и ее определитель равен 0. Если i=j, то получаем матрицу A. Таким образом, элемент матрицы произведения, расположенный на пересечении строки i и столбца j равен 0 при и 1 при i=j, то есть AB=E. Аналогично, проверяется равенство BA=E.Следовательно, матрица B – обратная к A.
Следствие 6.1 Если BA=E или AB=E, то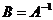 
.
Доказательство. Если BA=E, то матрица A – невырожденная, и к ней существует единственная обратная матрица. Далее,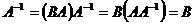 
или 
.
Правило Крамера
Рассмотрим систему линейных уравнений Ax=b, где матрица A невырожденная. Умножим слева это равенство на обратную матрицу, придем к равенству 
. Решение системы существует и единственно. Элемент обратной матрицы, расположенный на пересечении строки i и столбца j равен 
. Следовательно, i-ая компонента x равна 
. Сумма 
является разложением по столбцу i определителя матрицы, отличающейся от A столбцом i, равным b. Обозначим через 
значение этого определителя. Тогда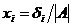 
. Оформим полученные результаты в виде теоремы.
Теорема 6.2 (Правило Крамера). Квадратная система уравнений с невырожденной матрицей имеет единственное решение, компоненты которого находятся по формулам 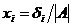, где значение определителя матрицы, отличающейся от A столбцом i, равным b.
