Пусть f(x) - неприводимый многочлен степени n над числовым полем P, и пусть 
корень этого многочлена в некотором числовом поле T (P содержится в T). Построим наименьшее поле, содержащее поле P и . Легко убедится, что числа вида 
, где 
принадлежат этому полю. Обозначим множество этих чисел 
.
Теорема 2.12 Множество является числовым полем.
Доказательство. Замкнутость относительно сложения, вычитания, умножения очевидна. Покажем замкнутость относительно деления. По числу 
построим многочлен 
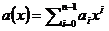из P(x). Наибольший общий делитель многочленов a(x) и f(x) равен 1 (в силу неприводимости f(x)), следовательно, найдутся многочлены u(x) и v(x) из P(x), что u(x)f(x)+v(x)a(x)=1. Подставим вместо x значение . Получим равенство 
. Поскольку 
, 
и 
, то теорема доказана.
В качестве можно брать любой корень многочлена f(x). В результате будут получаться различные поля .
Определение 2.3 Числовые поля называются изоморфными, если существует взаимно однозначное соответствие, сохраняющее операции +,*.
Следствие 2.5 Пусть f(x) - неприводимый многочлен над полем P, и a, b - его корни в некотором поле T. Тогда поле P(a) изоморфно полю P(b).
В приведённых выше построениях везде фигурировало поле T, которое содержало корень многочлена. Избавимся от этого поля. Это можно сделать следующим образом. Обозначим через P[x] множество остатков от деления многочленов из P(x) на неприводимый многочлен f(x) (над P). На этом множестве определим операции сложения и умножения. Сложение - обычное сложение многочленов, а в качестве результата умножения многочленов возьмём остаток от деления их произведения на f(x). В результате получим множество многочленов над которыми определены операции сложения и умножения, причём это множество изоморфно P(a), где a - корень f(x) в некотором поле T. При построении поля P[x] поле T никак не участвует.
Говорят, что поле P[x] получено присоединением корня f(x). При этом вопросом о существовании поля, в котором f(x) имеет корень, можно не задаваться. Следует отметить, что элемент x поля P[x] является корнем f(x).
Теорема 2.13 Пусть f(x) - многочлен над полем P. Тогда существует поле T (P содержится в T) над которым многочлен f(x) разлагается на линейные множители
Доказательство. Разлагаем f(x) на неприводимые множители. Если все множители линейны, то теорема доказана. В противном случае возьмём неприводимый многочлен степени больше 1 и присоединим его корень. Далее, повторим рассуждения. Процесс бесконечно продолжаться не может из-за конечности степени f(x).
Поле, над которым многочлен разлагается на линейные множители, называется полем разложения многочлена.
