Ряд задач алгебры приводит к задаче построения решения системы линейных уравнений. Например, вычисление коэффициентов интерполяционного многочлена методом неопределённых коэффициентов. В общем виде задача отыскания решения системы линейных уравнений выглядит следующим образом. Найти набор чисел 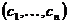 при подстановке которых вместо переменных
при подстановке которых вместо переменных  все уравнения системы
все уравнения системы  обращаются в равенства.
обращаются в равенства.
Запишем таблицу чисел, образованную коэффициентами при неизвестных  . В алгебре принято называть прямоугольную таблицу чисел матрицей. Припишем к матрице коэффициентов правые части уравнений
. В алгебре принято называть прямоугольную таблицу чисел матрицей. Припишем к матрице коэффициентов правые части уравнений  отделив их от матрицы коэффициентов вертикальной чертой. Получившаяся матрица называется расширенной матрицей системы линейных уравнений. В дальнейшем нам будет удобнее работать не с системой линейных уравнений, а с её расширенной матрицей.
отделив их от матрицы коэффициентов вертикальной чертой. Получившаяся матрица называется расширенной матрицей системы линейных уравнений. В дальнейшем нам будет удобнее работать не с системой линейных уравнений, а с её расширенной матрицей.
Равносильные преобразования
Обозначим через M множество решений системы линейных уравнений (элементами множества M являются n-элементные наборы, удовлетворяющие системе линейных уравнений). Преобразование системы линейных уравнений называется равносильным, если оно не меняет её множество решений. Аналогично, преобразование матрицы называется равносильным, если оно соответствует равносильному преобразованию системы линейных уравнений.
Теорема 3.1 Следующие преобразования матрицы являются равносильными:
I. Умножение строки не ненулевое число.
II. Перестановка строк
III. Прибавление к некоторой строке другой строки, умноженной на число.
Доказательство. Равносильность всех трёх преобразований доказывается по одному плану. Приведём этот план. Пусть M – множество решений исходной системы линейных уравнений, а T – множество решений преобразованной системы линейных уравнений (одним из трёх перечисленных преобразований). Взяв элемент x из M, подстановкой убедимся, что он принадлежит T. Тем самым покажем включение  . Далее, от новой системы линейных уравнений можно вернуться к исходной системе, выполнив обратное преобразование. Значит, по доказанному ранее
. Далее, от новой системы линейных уравнений можно вернуться к исходной системе, выполнив обратное преобразование. Значит, по доказанному ранее 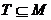 . Объединив оба включения получаем требуемое равенство.
. Объединив оба включения получаем требуемое равенство.
Метод Гаусса.
Теорема 3.2 Равносильными преобразованиями, указанными выше (Теорема 3.1) расширенную матрицу можно привести к ступенчатому виду.
Доказательство. Приведём алгоритм приведения матрицы к ступенчатому виду…..
После того как матрица приведена к ступенчатому виду легко построить решение системы линейных уравнений, либо доказать его отсутствие. Если матрица имеет строку, у которой только один ненулевой элемент, расположенный в последнем столбце, то решений нет. В противном случае решение есть и легко строиться.
Подстановки
Определение 4.1. Подстановкой n-го порядка называется взаимно однозначное отображение множества чисел от 1 до n на себя.
Подстановки можно записывать в виде таблицы, где под каждым числом стоит его образ. Например, подстановка 3 порядка  переводит 1 в 3, 2 в 1 и 3 в 2.
переводит 1 в 3, 2 в 1 и 3 в 2.
Лемма 4.1. Число подстановок n-го порядка равно n!.
Доказательство очевидно.
Определение подстановки, как взаимно однозначной функции позволяет перенести понятие суперпозиции функций на подстановки. Пусть подстановка f ставит в соответствие номеру i номер f(i), а подстановка g ставит в соответствие номеру j номер g(j). Рассмотрим функцию f(g(i)). Очевидно, эта функция задает взаимно однозначное отображение множества чисел от 1 до n, и, следовательно, определяет подстановку.
Определение 4.2. Подстановку, определенную функцией f(g(i)) называют суперпозицией или произведением подстановок g и f и обозначают gf.
Для примера найдем суперпозицию подстановок  и
и  . Поскольку f(g(1))=f(1)=2, f(g(2))=f(3)=3, f(g(3))=f(2)=1, то
. Поскольку f(g(1))=f(1)=2, f(g(2))=f(3)=3, f(g(3))=f(2)=1, то  .
.
Отметим некоторые свойства операции произведения подстановок.
Свойство 4.1 Операция произведения подстановок не коммутативна, то есть в общем случае  .
.
Действительно,  Свойство 4.2. Операция умножения подстановок ассоциативна, то есть f(gh)=(fg)h.
Свойство 4.2. Операция умножения подстановок ассоциативна, то есть f(gh)=(fg)h.
Доказательство. В подстановке f(gh) номер i отображается в номер (gh)(f(i))=h(g(f(i))), а в подстановке (fg)h номер i отображается в число h((fg)(i))=h(g(f(i))). В обоих случаях образ совпадает.
Определение 4.3Подстановка  называется тождественной, и обозначается e. Подстановка f называется обратной к подстановке g, если fg=e.
называется тождественной, и обозначается e. Подстановка f называется обратной к подстановке g, если fg=e.
Свойство 4.3. Обратная подстановка существует и единственна.
Доказательство очевидным образом следует из определения подстановки как взаимно однозначного соответствия.
Начиная с некоторого номера j, построим последовательность чисел  . В данной последовательности обязательно наступит повторение, поскольку множество значений подстановки
. В данной последовательности обязательно наступит повторение, поскольку множество значений подстановки  конечно. Пусть
конечно. Пусть  - наименьший номер, после которого появляется ранее встречавшееся число в последовательности (т.е.
- наименьший номер, после которого появляется ранее встречавшееся число в последовательности (т.е.  и k>s). Если
и k>s). Если  , то номер
, то номер  является образом двух номеров
является образом двух номеров  и
и 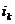 , что противоречит определению подстановки как взаимно однозначного соответствия. Следовательно,
, что противоречит определению подстановки как взаимно однозначного соответствия. Следовательно,  , и последовательность
, и последовательность  , начиная с
, начиная с  члена, начинает повторяться. Не повторяющаяся часть последовательности (т.е. её первые k+1 членов) называется циклом длины k+1.
члена, начинает повторяться. Не повторяющаяся часть последовательности (т.е. её первые k+1 членов) называется циклом длины k+1.
Циклы называются независимыми, если никакие два цикла не имеют общих номеров.
Кроме табличной записи подстановок существует их запись в виде произведения независимых циклов.
Часто удобно представлять подстановку в виде произведения независимых циклов, а не в табличном виде. В отличие от табличного вида подстановка пишется в строчку. За каждым номером i следует его образ f(i). Номера в цикле разделены тире. Циклы пишутся через запятую. Не пишутся также элементы, которые переходят сами в себя (т.е. циклы длины 1). Например, подстановка  запишется как (1-3), а подстановка
запишется как (1-3), а подстановка  запишется как (1-3-2, 4-5)
запишется как (1-3-2, 4-5)
Четность подстановок
Дискриминантом называется многочлен от n переменных  . Квадрат дискриминанта является симметрическим многочленом. Следовательно, при подстановке переменных может меняться только знак дискриминанта.
. Квадрат дискриминанта является симметрическим многочленом. Следовательно, при подстановке переменных может меняться только знак дискриминанта.
Определение 4.4. Подстановка f называется четной, если она не меняет знак дискриминанта (то есть  ), и нечетной в противном случае.
), и нечетной в противном случае.
Свойство 4.4. Четность произведения подстановок зависит от четности сомножителей. Произведение подстановок одинаковой четности всегда четно, а произведение подстановок разной четности – нечетно.
Выполнение подстановки сводится к последовательному выполнению подстановок сомножителей. Следовательно, знак подстановки равен произведению знаков сомножителей.
Определение 4.5. Подстановка, меняющая только два соседних по порядку номера, называется инверсией. Инверсия имеет вид (i-i+1).
Свойство 4.5. Инверсия является нечетной подстановкой.
Применив инверсию к дискриминанту, видим, что поменяется знак только у единственного сомножителя  . Следовательно, дискриминант меняет знак.
. Следовательно, дискриминант меняет знак.
Определение 4.6. Для подстановки f определим число нарушений порядка  как число всех пар, для которых i<j и f(i)>f(j).
как число всех пар, для которых i<j и f(i)>f(j).
Например, при 
 так как существуют только две пары на которых нарушается порядок. Это 1,2 (f(1)=3>f(2)=1) и 1,3 (f(1)>f(3)=2).
так как существуют только две пары на которых нарушается порядок. Это 1,2 (f(1)=3>f(2)=1) и 1,3 (f(1)>f(3)=2).
Теорема 4.1.Подстановка f представима в виде произведения  инверсий.
инверсий.
Доказательство проведем индукцией по 

. Для  существует единственная подстановка
существует единственная подстановка  . Если
. Если  , то подстановка сама является инверсией. Пусть утверждение теоремы верно при
, то подстановка сама является инверсией. Пусть утверждение теоремы верно при  . Покажем его справедливость при
. Покажем его справедливость при  . Найдем номер i для которого f(i)>f(i+1) (существование такого i очевидно). Подстановка (i-i+1)f имеет j нарушений порядка. По предположению индукции, эта подстановка представима в виде произведения j инверсий
. Найдем номер i для которого f(i)>f(i+1) (существование такого i очевидно). Подстановка (i-i+1)f имеет j нарушений порядка. По предположению индукции, эта подстановка представима в виде произведения j инверсий  . Из полученного равенства, умножив слева на (i-i+1), находим
. Из полученного равенства, умножив слева на (i-i+1), находим  . Подстановка f представлена в виде произведения j+1 инверсий, тем самым теорема доказана.
. Подстановка f представлена в виде произведения j+1 инверсий, тем самым теорема доказана.
Из теоремы вытекает, что четность подстановки совпадает с четностью числа нарушений порядка в ней.
Определение 4.7. Подстановка, меняющая только два элемента, называется транспозицией.
Лемма 4.2. Транспозиция является нечетной подстановкой.
Рассмотрим транспозицию (i-j), где i<j. Число нарушений порядка этой транспозиции равно 2(j-i)-1, всегда нечетное число.
Лемма 4.3. Четность цикла длины k равна четности числа k-1.
Доказательство проведем индукцией по длине цикла k. При k=2 утверждение доказано в предыдущей лемме. Пусть утверждение леммы верно при k-1. Покажем его справедливость для цикла длины k. Из равенства  следует, что четность цикла длины k равна четности цикла длины k-1 плюс 1, то есть четности k-1.
следует, что четность цикла длины k равна четности цикла длины k-1 плюс 1, то есть четности k-1.
Определение 4.8. Сумма длин независимых циклов минус количество циклов называется декрементом подстановки.
Разложив подстановку в произведение независимых циклов, определим её чётность.
Теорема 4.2. Четность подстановки равна ее декременту.
Определитель
Определение 5.1. Пусть A – квадратная матрица порядка n с элементами 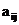 . Определителем матрицы A называется сумма по всем подстановкам
. Определителем матрицы A называется сумма по всем подстановкам  . Определитель (детерминант) матрицы обозначается
. Определитель (детерминант) матрицы обозначается  или det(A).
или det(A).
В частности определитель матрицы второго порядка вычисляется по формуле  , а определитель третьего порядка равен
, а определитель третьего порядка равен  . Вычисление определителей больших порядков исходя из определения не целесообразно.
. Вычисление определителей больших порядков исходя из определения не целесообразно.
Свойства определителя
Разберем свойства определителей.
Замену строк матрицы на ее столбцы назовем операцией транспонирования и обозначим через 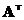 .
.
Свойство 5.1. Определитель матрицы не меняется при ее транспонировании.
Доказательство.  . Упорядочив сомножители в каждом слагаемом по возрастанию номеров строк, получим
. Упорядочив сомножители в каждом слагаемом по возрастанию номеров строк, получим  , где g обратная подстановка к f. Поскольку их произведение четная подстановка, то четность f и g совпадают и
, где g обратная подстановка к f. Поскольку их произведение четная подстановка, то четность f и g совпадают и  . Когда f пробегает все подстановки, то g пробегает все подстановки. От подстановки слагаемых сумма не меняется, поэтому
. Когда f пробегает все подстановки, то g пробегает все подстановки. От подстановки слагаемых сумма не меняется, поэтому  .
.
Свойство 5.2. При перестановке двух строк определитель матрицы изменит знак.
Доказательство. Пусть матрица B получена из матрицы A перестановкой строк с номерами i и j. Транспозицию (i-j) обозначим через  . Имеет место равенство
. Имеет место равенство  . Выразим определитель матрицы B через элементы матрицы A
. Выразим определитель матрицы B через элементы матрицы A  . Учитывая равенство
. Учитывая равенство  и тот факт, что когда f пробегает всё множество подстановок
и тот факт, что когда f пробегает всё множество подстановок  , то
, то  тоже пробегает все множество подстановок выводим требуемое свойство.
тоже пробегает все множество подстановок выводим требуемое свойство.
Свойство 5.3. Если матрица имеет две одинаковые строки, то ее определитель равен 0.
Доказательство. При подстановке одинаковых строк матрица не меняется, а значит, не изменится её определитель. По доказанному ранее, определитель должен поменять знак. Выполнение этих условий возможно в единственном случае, определитель равен нулю.
Свойство 5.4. Определитель не изменится, если к строке прибавить другую строку умноженную на число.
Доказательство. Пусть матрица B получена из матрицы A прибавлением к строке i строки j, умноженной на число c. Выразим определитель матрицы B через элементы матрицы A  . Раскроем скобки и подставим слагаемые, получим
. Раскроем скобки и подставим слагаемые, получим  . Сумма
. Сумма  является определителем матрицы, у которой две строки равны (I и j), и, значит, равна нулю. Таким образом,
является определителем матрицы, у которой две строки равны (I и j), и, значит, равна нулю. Таким образом,  .
.
Свойство 5.5. Определитель треугольной матрицы равен произведению диагональных элементов.
Доказательство. Пусть матрица A имеет верхнее треугольный вид, т.е 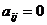 при i<j. Определитель матрицы равен
при i<j. Определитель матрицы равен  . Если
. Если 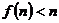 , то
, то  , поэтому в сумме ненулевое слагаемое только при
, поэтому в сумме ненулевое слагаемое только при  . Поскольку
. Поскольку  , то аналогично рассуждая, получаем
, то аналогично рассуждая, получаем  . И так далее. В результате, сумма содержит только одно ненулевое слагаемое, соответствующее тожественно подстановке, и, значит
. И так далее. В результате, сумма содержит только одно ненулевое слагаемое, соответствующее тожественно подстановке, и, значит  . Если матрица имеет нижнее треугольный вид, то транспонированием приведём её к верхнее треугольному виду, а потом применим Свойство 5.5.
. Если матрица имеет нижнее треугольный вид, то транспонированием приведём её к верхнее треугольному виду, а потом применим Свойство 5.5.
Поскольку при транспонировании определитель матрицы не меняется, а преобразования со строками становятся преобразованиями со столбцами, то тем самым установлено
Свойство 5.6 Определитель матрицы
1. изменит знак при перестановке столбцов
2. равен нулю, если имеется два одинаковых столбца
3. не изменится при прибавлении к столбцу другого столбца, умноженного на число.






