В ряде случаев необходимо найти многочлен наименьшей степени, у которого на некотором множестве заданы не только его значения, но и значения производных до определенных порядков. Пусть на множестве точек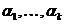 
заданы значения функции и её производных высших порядков. Под 
будем понимать значение производной порядка i в точке 
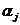. Под производной порядка 0 будем понимать саму функцию. Пусть заданы значения , где j=1,…,k и 
.
Теорема 2.16 (Интерполяционный многочлен Лагранжа - Сильвестра)
Существует единственный многочлен h(x) степени меньше 
, удовлетворяющий равенствам 
, где j=1,…,k и .
Доказательство. Положим 
, 
. Для i=1,…,k определим числа 
и далее по индукции 
, где 
. Многочлен 
удовлетворяет равенствам: 
при 
и 
, и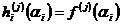 
. Что бы убедится в справедливости равенств найдём производную j порядка 
. Поскольку 
при 
и 
, то равенства при и установлены. Подставим теперь 
и получим 
Подставив вместо 
равное ему выражение, после приведения подобных, получим равенство 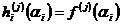. Далее осталось написать интерполяционный многочлен 
. Поскольку степень каждого слагаемого меньше , то и степень суммы меньше . Единственность интерполяционного многочлена покажем методом от противного. Допустим, существует два интерполяционных многочлена h(x) и g(x). Их разность имеет 
корнем кратности не меньше 
и значит, делится на w(x) без остатка. Поскольку степень w(x) заведомо больше чем степень h(x)-g(x), то h(x)=g(x).
Формулы Виета
Теорема 2.17 (Формулы Виета) Пусть многочлен 
имеет корни 
. Тогда 
.
Симметрические полиномы
Определение 2.4Многочленом от n переменных называется функция вида 
. Степенью многочлена называется максимальная суммарная степень по всем переменным. Слагаемое вида 
называется мономом.
Многочлен от n переменных может содержать несколько мономов максимальной степени. Моном максимальной степени назовём старшим, если набор его степеней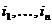 
лексикографически максимален. Обозначим через v(f) набор степеней максимального монома. Имеет место
Лемма 2.2 v(fg)=v(f)+v(g), 
Доказательство вытекает из определения.
Определение 2.5Многочлен от нескольких переменных называется симметрическим, если он не меняется при любой перестановке переменных.
Определение 2.6Многочлены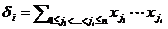 
, где i=1,…,n называются элементарными симметрическими многочленами.
Коэффициенты многочлена с точностью до знака суть значения элементарных симметрических многочленов от его корней.
Заметим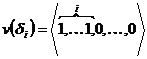 
.
Лемма 2.3 Пусть f - симметрический многочлен и 
, тогда 
.
Доказательство. Если найдётся i, при котором 
, то переставим 
и 
. В результате получим более старший моном.
Лемма 2.4 Пусть - набор целых неотрицательных чисел. Тогда 
.
Доказательство проводится непосредственно проверкой.
Теорема 2.18 (Основная теорема алгебры симметрических многочленов)
Любой симметрический многочлен единственным образом представляется в виде полинома от элементарных симметрических многочленов.
Доказательство. Пусть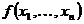 
- симметрический многочлен и . Обозначим через 
коэффициент при старшем мономе f и положим 
. Многочлен g симметрический и v(g) лексикографически меньше v(f). Следовательно, через конечное число шагов он станет равный нулю и f выразится в виде полинома от элементарных симметрических многочленов.
Допустим, существуют два разных представления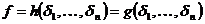 
. Разность f-g - не нулевой многочлен от элементарных симметрических многочленов, но при выражении элементарных симметрических многочленов через переменные он должен обратиться в 0.
Выделим член 
, у которого величина 
максимальная. Если таких членов несколько, то из них выберем такое, на котором набор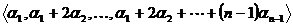 
лексикографически максимален. Набор, отвечающий данным условиям единственен. При подстановке переменных вместо элементарных симметрических полиномов именно этот набор даст старший моном. Причём это моном входит только в единственное слагаемое. Следовательно, найдётся моном с отличным от нуля коэффициентом, что противоречит равенству f-g=0.
Формулы Кардано
Обозначим корни кубического уравнения 
через 
. Положим 
и 
, 
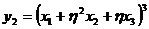. Легко проверить, что 
и 
, 
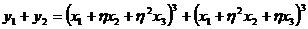- симметрические многочлены от . По основной теореме алгебры симметрических многочленов их можно выразить через элементарные симметрические многочлены, значения которых, по формулам Виета, совпадают с точностью до знака с коэффициентами исходного многочлена. Проведя несложные вычисления, получим 
и 
. По формулам Виета 
- корни квадратного уравнения 
и могут быть вычислены по формулам 
. Таким образом справедливы уравнения 
, 
, 
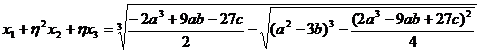. Из этой системы находим корни исходного уравнения.
Способ Феррари
Обозначим корни уравнения 
через 
. Положим 
, 
, 
. Легко проверить, что перестановка переменных приводит лишь к некоторой перестановке 
и поэтому, элементарные симметрические многочлены от являются симметрическими многочленами от . Следовательно, можно написать уравнение третей степени, коэффициенты которого суть многочлены от коэффициентов исходного многочлена, корнями которого являются . Кубическое уравнение называют кубической резольвентой. После нахождения корней , из уравнения 
(к нему сводится решение системы , 
) находим 
, из уравнения 
- 
, и из уравнения 
- 
. Выразив все корни через 
и подставив выражения в уравнение 
найдём все корни исходного уравнения.
Дискриминант
Дискриминантом называется многочлен от n переменных 
. Квадрат дискриминанта является симметрическим многочленом.
Основная теорема Алгебры
Лемма 2.5. Многочлен нечётной степени с вещественными коэффициентами имеет хотя бы один вещественный корень.
Доказательство. Не нарушая общности можно считать старший коэффициент многочлена равным 1. Пусть 
, и 
. Тогда справедливы неравенства 
и 
. На концах отрезка 
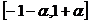многочлен f(x) принимает значения, противоположные по знаку, следовательно, найдётся такое число , что 
.
Лемма 2.6. Многочлен второй степени с комплексными коэффициентами имеет комплексные корни.
Доказательство очевидно.
Лемма 2.7 Многочлен с вещественными коэффициентами имеет хотя бы один комплексный корень.
Доказательство. Любое натуральное число, а, значит и степень многочлена n, можно представить в виде произведения 
, где m – нечётное число. Доказательство проведём методом математической индукции по s. Если s=0, то n – нечётно, и утверждение следует из приведённой выше леммы. Пусть утверждение леммы справедливо для s-1. Покажем его справедливость для s. Рассмотрим многочлен f(x) степени . Построим его поле разложения. В этом поле он имеет корни 
. Для некоторого вещественного числа q построим многочлен 
. Коэффициенты этого многочлена являются симметрическими многочленами от , а значит многочленами (с вещественными коэффициентами) от коэффициентов f(x). Степень 
равна 
, и по предположению индукции многочлен имеет комплексный корень. Не нарушая общности, можно считать, что найдутся различные вещественные числа 
и 
, при которых числа 
и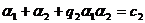 
- комплексные. Но тогда 
и 
. Многочлен второй степени 
имеет комплексные коэффициенты, а значит и его корни 
. Тем самым лемма доказана.
Теорема 2.19 (Основная теорема алгебры)
Любой многочлен над полем комплексных чисел имеет хотя бы один комплексный корень.
Доказательство. Пусть f(x) многочлен с комплексными коэффициентами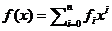 
. Положим 
и 
. У многочлена g(x) - вещественные коэффициенты, и по доказанному выше, g(x) имеет комплексный корень a, то есть 
. Если f(a)=0, то теорема доказана, a – корень f(x). Пусть 
. По свойствам операции сопряжения 
, откуда выводим 
корень f(x).
Следствие 2.8 Многочлен над полем комплексных чисел разлагается в произведение линейных множителей. Разложение единственно с точностью до перестановки сомножителей.
Доказательство. По основной теореме алгебры многочлен f(x) над полем комплексных чисел имеет комплексный корень a, и по теореме Безу, делится на двучлен x-a. Поделим f(x) на x-a и повторим указанные действия с частным. В результате разложим многочлен на линейные множители. Единственность разложения доказана ранее (Теорема 2.8).
