Определение 2.2Многочлен над кольцом целых чисел называется примитивным, если наибольший общий делитель его коэффициентов равен 1.
Многочлен с рациональными коэффициентами единственным образом представляется в виде произведения положительного рационального числа и примитивного многочлена. Рациональное число называют содержанием многочлена.
Теорема 2.10 Произведение примитивных многочленов есть примитивный многочлен.
Доказательство проведём методом от противного. Пусть произведение двух примитивных многочленов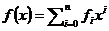 
и 
есть не примитивный многочлен 
. Найдётся простое число p, которое делит все коэффициенты многочлена h(x) без остатка. Пусть 
-самый младший (с наименьшим номером) коэффициент f(x), не делящийся на p без остатка (такой найдётся в силу примитивности многочлена), а 
- самый младший коэффициент g(x), не делящийся на p без остатка. Коэффициент многочлена h(x) при 
вычисляется по формуле 
. Слагаемое 
делится на p без остатка при s<i, так как левый множитель кратен p, а при s>i, так как правый множитель кратен p. Единственное слагаемое, которое не делится на p, получается при s=i. Следовательно, вся сумма не делится на p, а значит не все коэффициенты h(x) делятся на p, что противоречит сделанному допущению. Тем самым теорема доказана.
Следствие 2.2. Если многочлен с целочисленными коэффициентами приводим над полем рациональных чисел, то он приводим над кольцом целых чисел.
Доказательство. Разложим многочлен над полем рациональных чисел. Каждый множитель представим в виде произведения его содержания и примитивного многочлена. Произведение примитивных многочленов суть примитивный многочлен, поэтому произведение содержаний множителей равно содержанию исходного многочлена. Для завершения доказательства осталось заметить, что содержание исходного многочлена есть целое число.
Таким образом, задача разложения многочлена на неприводимые множители над полем рациональных чисел сводится к аналогичной задаче над кольцом целых чисел.
Критерий Эйзенштейна
Теорема 2.11 (Критерий Эйзенштейна) Пусть f (x) многочлен над кольцом целых чисел. Если существует простое число p, что
I. Все коэффициенты многочлена f (x), кроме старшего, делятся на p
II. Старший коэффициент не делится на p
III. Свободный член не делится на 
Тогда многочлен f (x) неприводим над полем рациональных чисел.
Доказательство проведём методом от противного. Допустим многочлен h(x) удовлетворяет условиям теоремы и тем не менее представим в виде произведения двух многочленов f(x)g(x). Естественно, все многочлены с целыми коэффициентами. Поскольку 
, то либо 
делится на p, либо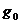 
делится на p (оба сразу делиться не могут, из-за условия III). Пусть, для определённости делится на p, а 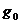не делится на p. Из равенства 
, делимости и 
на p, и не делимости 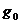на p, выводим делимость 
на p. Продолжив рассуждения, придём к тому, что все коэффициенты f(x) делятся на p, что противоречит условию I.
Следует отметить, что критерий Эйзенштейна даёт достаточные условия неприводимости многочленов, но не необходимые. Так многочлен 
является неприводимым над полем рациональных чисел, но не удовлетворяет критерию Эйзенштейна.
Следствие 2.3 Над полем рациональных чисел найдётся неприводимый многочлен степени n, где n любое натуральное число больше 1.
Действительно, многочлен 
, по критерию Эйзенштейна, является неприводимым.
Следствие 2.4 Для простого n многочлен 
неприводим над полем рациональных чисел.
Доказательство. Разложим многочлен по степеням x-1 
. Многочлен 
удовлетворяет критерию Эйзенштейна, и, значит, является неприводимым. Но тогда неприводим и многочлен 
.
