Бином Ньютона, треугольник Паскаля

Числа.

Натуральные числа

Определение 1.1Определение натуральных чисел N

1 - натуральное число. Если n - натуральное число, то следующее за ним n+1 так же натуральное число. Если кодировать натуральное число количеством чёрточек, равных этому числу, то под операцией + можно понимать просто приписывание очередной чёрточки. Далее, операция + распространяется на всё множество натуральных чисел. Операция + равносильна приписыванию к одной последовательности чёрточек, обозначающей первое слагаемое, другой последовательности чёрточек, обозначающей второе слагаемое. Отметим свойства данной операции

1. (a+b)+c=a+(b+c) - ассоциативность

2. a+b=b+a – коммутативность

Кроме операции + на множестве натуральных чисел определяется операция *. Операция определяется через сложение . Свойства операции умножения:

1. a*(b*c)=(a*b)*c – ассоциативность
2. a*b=b*a – коммутативность
3. a*(b+c)=a*b+a*c - дистрибутивность

Метод математической индукции.

Тот факт, что множество натуральных чисел может быть упорядочено по возрастанию часто используется при доказательстве математических утверждений. Допустим, у нас имеется серия утверждений, пронумерованных натуральными числами A₁,…,A_n…, и установлена истинность утверждения A₁ (основание мат. индукции), а так же показана справедливость посылки A_n-1®A_n в предположении истинности утверждений A₁,…,A_n-1 для любого натурального числа n. Выполнение этих условий гарантирует истинность всех утверждений A₁,…,A_n. Для примера покажем справедливость формулы .

При n=1 формула принимает вид , верно. Пусть формула верна для n-1. Покажем её справедливость для n.  Следующий пример связан с биномом Ньютона.

Бином Ньютона, треугольник Паскаля

Рассмотрим бином (a+b)ⁿ. Если раскрыть скобки, привести подобные, то получившиеся сумма состоит из слагаемых вида aⁱb^n-i с некоторыми числовыми коэффициентами. Например: (a+b)²=a²b⁰+2ab+a⁰b². В общем случае можно записать 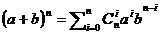, где  - числовой коэффициент. Из тождества (a+b)ⁿ=(a+b)(a+b)^n-1 выводим равенства  и , которые позволяют строить треугольник Паскаля. Приведём первые его 4 строки . Число, расположенное в треугольнике Паскаля на пересечении строки n и столбца m, равно

· 1, если m=0, или m=n,

· сумме элементов предыдущей строки, расположенных в столбцах m и m-1, если .

Таким образом, элементы треугольника Паскаля суть биномиальные коэффициенты. В частности .

Обозначим через  произведение натуральных чисел от 1 до n. Для удобства обозначений положим .

Теорема 1.1 Биномиальный коэффициент вычисляется по формуле .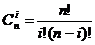

Доказательство проводится индукцией по n. При n=1 утверждение очевидно. Пусть оно верно при n-1. Покажем его справедливость для n. Если m=0, то . Если m=n, то . Если , то . По предположению индукции . Теорема доказана.

Целые числа

Решение уравнений вида a+x=b приводит к получению целых чисел Z. При этом следует отметить, что уравнение a+c+x=b+c имеет то же самое решение. На множество целых чисел естественным образом переносятся операции + и *, обладающими теми же самыми свойствами.

Рациональные числа

Решение уравнений вида a*x=b (a¹0) приводит к получению рациональных чисел Q. Уравнение a*c*x=b*c имеет то же самое решение. На множество рациональных чисел естественным образом переносятся операции + и *.

Числовые кольца, поля

Множество чисел, замкнутых относительно операции +, *, и в котором разрешимо уравнение a+x=b называется числовым кольцом.

Любое числовое кольцо содержит 0.

Множество чётных чисел - кольцо без 1

Числовое кольцо, в котором разрешимо уравнение ax=b (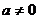) называется числовым полем.

Теорема 1.2 В любом числовом поле содержится поле рациональных чисел.

Доказательство. Пусть 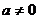 - элемент этого поля. Тогда  принадлежит полю, а значит в силу замкнутости относительно операции + и все натуральные числа. Поскольку уравнение a+x=b разрешимо для всех элементов поля, то в нём содержатся все целые числа. Аналогично, из разрешимости уравнения ax=b вытекает, что в поле содержатся все рациональные числа.

Кроме поля рациональных чисел существуют другие поля. Например: числа вида  образуют числовое поле.

Вещественные числа

Вещественным числом называется бесконечная десятичная дробь. Множество вещественных чисел является полем

Поле комплексных чисел

Положим . Числа вида , где  называются комплексными. С комплексными числами возможны операции сложения, вычитания, умножения и деления.

Множество комплексных чисел образует поле комплексных чисел.

Представление комплексного числа в виде  называется его алгебраической формой. Коэффициенты a и b называются вещественной и мнимой частью комплексного числа, соответственно. Вещественную часть комплексного числа c обозначают Re (c), а мнимую часть – Im (c). Число  называют комплексно сопряженным к числу c и обозначают . Отметим, что комплексно сопряженное к сумме, разности, произведению и частному комплексных чисел есть сумма, разность, произведение и частное комплексно сопряженных чисел.

Комплексная плоскость.

Комплексному числу c поставим в соответствие точку плоскости c координатами (Re (c), Im (c)). Это соответствие взаимно однозначное. Для вектора, соединяющего начало координат, с этой точкой определено понятие длины и угла с осью, по которой откладывается вещественная часть. Длину вектора называют модулем комплексного числа и обозначают , а угол называют аргументом комплексного числа и обозначают Arg (c). Имеют место соотношения , , . Из них получаем тригонометрическую форму комплексного числа . Данная форма полезна при вычислении произведения и частного комплексных чисел.

Теорема 1.3 Пусть 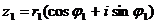 и , тогда  и .

Доказательство теоремы вытекает из тригонометрических тождеств и правил проведения соответствующих операций над комплексными числами в алгебраической форме.

Из данной теоремы вытекает

Теорема 1.4 (Формула Муавра-Лапласа) Для целого n и 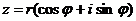 справедливо .