Метод наименьших квадратов.
Эти уравнения можно получить методом наименьших квадратов:
 , где
, где 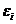 -некоторая ошибка измерений,
-некоторая ошибка измерений, 
Метод наименьших квадратов или метод Гаусса сводиться к тому, что коэффициенты 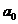 и
и  нужно искать из того, что сумма квадратов ошибок стремиться к минимуму, т.е.
нужно искать из того, что сумма квадратов ошибок стремиться к минимуму, т.е.
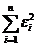 →min по всем наблюдениям.
→min по всем наблюдениям.
Для этого составляется функция F( )=
)=  .
.
Берутся частные производные от F( ) по
) по 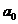 и
и  и приравнивают их к 0.
и приравнивают их к 0.


Составляется система из 2-х уравнений с 2-мя неизвестными, откуда и находятся 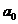 и
и 
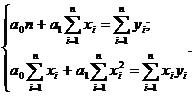 ;
; 
Следовательно, получаем уравнение линейной регрессии Y на X: 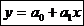
Тема 2.7 Планирование и анализ эксперимента
2.7.1 Задача планирования эксперимента.
2.7.2 Модель объекта.
2.7.3 Выбор факторов. Полный факторный эксперимент.
Задача планирования эксперимента.
Дисперсионный анализ.
Опр: Дисперсионным анализом называют статистический метод анализа результатов измерений, зависящих от различных одновременно действующих факторов.
Ограничимся рассмотрением простейшего случая, когда действует один фактор. Пусть, например, выборка разбита на r групп, причем i-я группа содержит  величин
величин 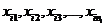 Предположим, что все указанные величины распределены нормально и
Предположим, что все указанные величины распределены нормально и 
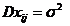 , j=1,…,
, j=1,…,  ; i=1,…,r.
; i=1,…,r.
Нам нужно проверить гипотезу, согласно которой  .
.
В физической постановке эта задача выглядит так: одна и та же величина a измеряется r различными приборами, имеющими одинаковую точность. Нас интересует, имеют ли приборы различные систематические ошибки. В рассматриваемом примере исследуется влияние одного фактора(прибора) на погрешность измерения. Введем следующие обозначения:  ,
, 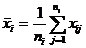 , n=
, n= 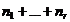 .
.
Групповые средние  являются несмещенными и состоятельными оценками величин
являются несмещенными и состоятельными оценками величин  .
.
Если все  одинаковы, то общая средняя не должна сильно отличаться от групповых. В противном случае разброс
одинаковы, то общая средняя не должна сильно отличаться от групповых. В противном случае разброс  относительно
относительно  должен быть более значительным. Представим общую, или полную, сумму квадратов отклонений:
должен быть более значительным. Представим общую, или полную, сумму квадратов отклонений: 
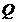 =
= 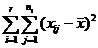 (1)
(1)
в следующем виде: 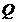 =
=  (2) , где
(2) , где
 =
= 
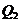 =
= 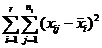 . (3)
. (3)
Равенство (2) следует из (1), если воспользоваться формулами:
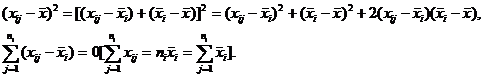
Опр: Сумму  называют суммой квадратов отклонений “между группами”,
называют суммой квадратов отклонений “между группами”, 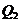 - суммой квадратов отклонений “внутри групп”.
- суммой квадратов отклонений “внутри групп”.
По лемме Фишера величина 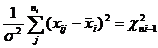 , следовательно,
, следовательно, 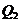 имеет распределение
имеет распределение 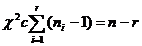 степенями свободы.
степенями свободы.
Можно показать, что если  , то
, то  и
и 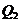 независимы и
независимы и 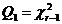 . Следовательно, при
. Следовательно, при 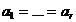 величина
величина
 . (4)
. (4)
имеет распределение Фишера с r-1, n-r состояниями свободы. Величина (4) может быть использована для проверки гипотезы о равенстве математических ожиданий
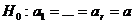 . Если эта гипотеза верна, то
. Если эта гипотеза верна, то  и
и  являются состоятельными оценками одной и той же случайной величины
являются состоятельными оценками одной и той же случайной величины  и, следовательно, близки между собой, а величина
и, следовательно, близки между собой, а величина  мала. Если
мала. Если  различны, то
различны, то 
 и
и  сближаются с разными математическими ожиданиями:
сближаются с разными математическими ожиданиями:
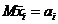 ,
, 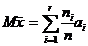
и, следовательно, сумма  должна принимать большие значения. Независимо от предложения о равенстве
должна принимать большие значения. Независимо от предложения о равенстве  ,знаменатель в (4) остается оценкой σ². Это означает, что при увеличении расхождения между
,знаменатель в (4) остается оценкой σ². Это означает, что при увеличении расхождения между  величина (4) в среднем должна принимать большие значения. Статистический критерий формулируется следующим образом: если
величина (4) в среднем должна принимать большие значения. Статистический критерий формулируется следующим образом: если 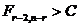 , то гипотеза
, то гипотеза 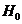 отвергается. Здесь С определяется по таблице распределения Фишера с уровнем значимости
отвергается. Здесь С определяется по таблице распределения Фишера с уровнем значимости 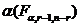
Методы расчета сводных характеристик выборки.
Условные варианты.
Предположим, что варианты выборки расположены в возрастающем порядке, т.е. в виде вариационного ряда.
Опр: Равностоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.
Опр: Условными называют варианты, определяемые равенством:

где С- ложный нуль (новое начало отсчета); h- шаг, т.е. разность между любыми двумя соседними первоначальными вариантами(новая единица масштаба).
Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условными.
Покажем, что если вариационный ряд состоит из равностоящих вариант с шагом h, то условные варианты есть целые числа. Действительно, выберем в качестве ложного нуля произвольную варианту, например 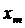 , тогда
, тогда
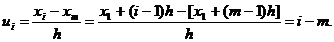
Т.к. i и m –натуральные числа, то их разность i-m= 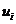 -также целое число.
-также целое число.
Замечание 1. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда(часто такая варианта имеет наибольшую частоту).
Замечание2. Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная 0.
Пример: Найти условные варианты статистического распределения:

| 23,6 | 28,6 | 33,6 | 38,6 | 43,6 |

| 5 | 20 | 50 | 15 | 10 |
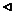 Выберем в качестве ложного нуля С варианту 33,6(она расположена в середине вариационного ряда). Найдем шаг h=28,6-23,6=5. Найдем условную варианту:
Выберем в качестве ложного нуля С варианту 33,6(она расположена в середине вариационного ряда). Найдем шаг h=28,6-23,6=5. Найдем условную варианту:
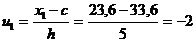
Аналогично получаем 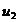 =-1;
=-1; 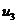 =0;
=0;  =1;
=1; 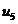 =2. Видим, что условные варианты – небольшие целые числа. Оперировать с ними проще, чем с первоначальными вариантами.
=2. Видим, что условные варианты – небольшие целые числа. Оперировать с ними проще, чем с первоначальными вариантами. 
Обычные, начальные и центральные эмпирические моменты.
Для вычисления основных характеристик выборки удобно пользоваться эмпирическими моментами, определения которых аналогичны определениям соответствующих теоретических моментов. В отличие от теоретических, эмпирические моменты вычисляют по данным наблюдений.
Опр: Обычным эмпирическим моментом порядка к называют среднее значение к-х степеней разностей  :
:

где  - наблюдаемая варианта,
- наблюдаемая варианта,  -частота варианты, n=
-частота варианты, n=  -объем выборки, С-произвольное постоянное число(ложный нуль).
-объем выборки, С-произвольное постоянное число(ложный нуль).
Опр: Начальным эмпирическим моментом порядка к называют обычный момент порядка к при С=0
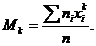
В частности 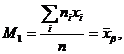 т.е. начальный эмпирический момент первого порядка равен выборочной средней.
т.е. начальный эмпирический момент первого порядка равен выборочной средней.
Опр: Центральным эмпирическим моментом порядка к называют обычный момент порядка к при  :
:
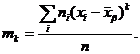
Например,  ,
,
т.е. центральный эмпирический момент второго порядка равен выборочной дисперсии.
Условные эмпирические моменты. Отыскание центральных моментов по условным.
Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упростить расчеты, заменяют первоначальные варианты условными.
Опр: Условным эмпирическим моментом порядка к называют начальный момент порядка к, вычисленный для условных вариант:
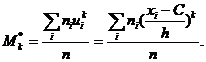
В частности,
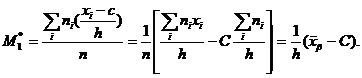
Таким образом, чтобы найти выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на h и к результату прибавить ложный нуль С.
 .
.
По определению, условный момент к-го порядка
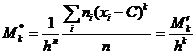 .
.
Отсюда 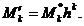
Таким образом, чтобы найти обычный момент порядка к, нужно условный момент того же порядка
умножить на 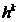 . Выборочная дисперсия вычисляется по формуле:
. Выборочная дисперсия вычисляется по формуле:

Модель объекта.
Метод произведений для выборочной средней и дисперсии.
Метод произведений даёт удобный способ вычисления условных моментов различных порядков для вариационного ряда с равностоящими вариантами. Зная условные моменты, нетрудно найти начальные и центральные эмпирические моменты. В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется так:
в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;
во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца;
в третий столбец записывают условные варианты  , причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над 0 пишут последовательно -1, -2, -3 и т. д., а под 0 – 1,2, 3 …;
, причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над 0 пишут последовательно -1, -2, -3 и т. д., а под 0 – 1,2, 3 …;
умножают частоты на условные варианты и записывают их произведение  в четвертый столбец; сложив все полученные числа, их сумму
в четвертый столбец; сложив все полученные числа, их сумму 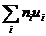 помещают в нижнюю клетку столбца;
помещают в нижнюю клетку столбца;
умножают частоты на квадраты условных вариант и записывают их произведение  в пятый столбец; сложив все полученные числа, их суму
в пятый столбец; сложив все полученные числа, их суму  помещают в нижнюю клетку столбца;
помещают в нижнюю клетку столбца;
умножают частоты на квадраты условных вариант, увеличенных на единицу, и записывают произведения 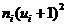 в шестой контрольный столбец; сложив все полученные числа, их сумму
в шестой контрольный столбец; сложив все полученные числа, их сумму  помещают в нижнюю клетку столбца.
помещают в нижнюю клетку столбца.
2.7.3 Выбор факторов. Полный факторный эксперимент. Замечание1. Целесообразно отдельно складывать отрицательные числа четвертого столбца (их суму  записывают в клетку строки, содержащей ложный нуль) и отдельно положительные числа (их сумму
записывают в клетку строки, содержащей ложный нуль) и отдельно положительные числа (их сумму 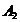 записывают в предпоследнюю клетку столбца); тогда
записывают в предпоследнюю клетку столбца); тогда 

Замечание2. При вычислении произведений  5-го столбца целесообразно числа
5-го столбца целесообразно числа  четвертого столбца умножить на
четвертого столбца умножить на 
Замечание3. 6 столбец служит для контроля вычислений: если сумма 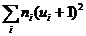 окажется равной сумме
окажется равной сумме 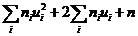 (как и должно быть в соответствии с тождеством
(как и должно быть в соответствии с тождеством 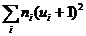 =
= 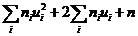 ), то вычисления проведены правильно.
), то вычисления проведены правильно.
После заполнения таблицы и проверки правильности вычислений, вычисляются условные моменты:

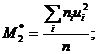
И вычисляют выборочные среднюю и дисперсию по формулам:
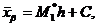
 .
.
Пример: Найти методом произведений выборочную среднюю и выборочную дисперсию следующего статистического распределения:

| 10,2 | 10,4 | 10,6 | 10,8 | 11,0 | 11,2 | 11,4 | 11,6 | 11,8 | 12 |

| 2 | 3 | 8 | 13 | 25 | 20 | 12 | 10 | 6 | 1 |
Составим расчетную таблицу:
записываем варианты в первый столбец;
запишем частоты во 2 столбец; сумму частот (100) поместим в нижнюю клетку столба;
в качестве ложного нуля С=11,0; в клетках пишем цифры от -4 до 5;
 находим, сумма отрицательных чисел
находим, сумма отрицательных чисел  =-46 и сумма положительных
=-46 и сумма положительных 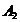 =103,
=103, 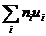 =57;
=57;
 находим, умножая 3 на 4 столбец, сумма чисел столбца (383) –в нижней клетке;
находим, умножая 3 на 4 столбец, сумма чисел столбца (383) –в нижней клетке;
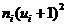 -6 контрольный столбец; сумму597 чисел столбца помещаем в нижнюю клетку столбца.
-6 контрольный столбец; сумму597 чисел столбца помещаем в нижнюю клетку столбца.
Контроль: 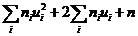 =383+2*57+100=597.
=383+2*57+100=597.
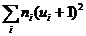 =597- правильно.
=597- правильно.
Вычислим условные моменты 1 и 2 порядков:

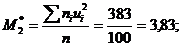
Шаг h=10,4-10,2=0,2
Искомые выборочные:

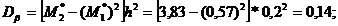
| 1 | 2 | 3 | 4 | 5 | 6 |

| 
| 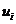
|  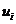
| 
| 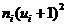
|
| 10,2 | 2 | -4 | -8 | 32 | 18 |
| 10,4 | 3 | -3 | -9 | 27 | 12 |
| 10,6 | 8 | -2 | -16 | 32 | 8 |
| 10,8 | 13 | -1 | -13 | 13 | 0 |
| 11,0 | 25 | 0 | 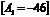
| 25 | |
| 11,2 | 20 | 1 | 20 | 20 | 80 |
| 11,4 | 12 | 2 | 24 | 48 | 108 |
| 11,6 | 10 | 3 | 30 | 90 | 160 |
| 11,8 | 6 | 4 | 24 | 96 | 150 |
| 12,0 | 1 | 5 | 5 | 25 | 36 |

| |||||
| n=100 | 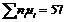
| 
| 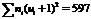
|






