Эмпирическая функция распределения.
Полигон и гистограмма.
Предположим, что имеется выборка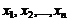 
из генеральной совокупности с функцией распределения F(x). Через Y обозначим случайную величину, принимающую значения 
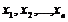с вероятностями 1/n.
| . | ||||
О. Случайная величина Y называется выборочной или эмпирической. Ряд распределения случайной величины Y называется выборочным или эмпирическим.
О. Числовые характеристики теоретической СВ Х называются генеральными характеристиками.
О. Числовые характеристики эмпирической случайной величины Y называются выборочными.
О. Генеральным начальным элементом к-го порядка называется число bk = MXk.
О. Выборочным начальным моментом к-го порядка называется число
.
О. Выборочной средней называется среднее арифметическое выборочного ряда распределения, т.е. 
.
О. Генеральным центральным моментом к-го порядка называется число
mk=M(X-MX)k
О. Выборочным центральным моментом к-го порядка называется число
.
В частности,
-
- выборочная дисперсия.
- оценка генеральной дисперсии 
.
О. Эмпирической функцией распределения называется функция распределения выборочной (эмпирической) случайной величины Y. Обозначается эта функция: 
.
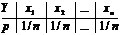
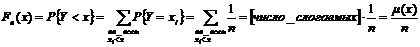, где 
- число выборочных значений 
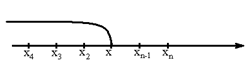
О. Последовательность значений 
, записанных в возрастающем порядке 
, где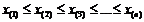 
, называется вариационным рядом выборки.
Пусть из генеральной совокупности извлечена выборка, причем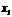 
наблюдалось 
раз, 
раз, …, 
раз и 
- объем выборки.
О. Наблюдаемые значения 
называют вариантами.
Числа наблюдений 
называют частотами, а их отношения к объему выборки 
- относительными частотами.
О. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот попавших в этот интервал вариант).
Замечание В теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями.
В МС – соответствие между наблюдаемыми вариантами и их частотами или относительными частотам.
Пример 1 Задано распределение частот выборки объема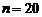 
:
Написать распределение относительных частот.
Решение Найдем относительные частоты, для чего разделим частоты на объем выборки:
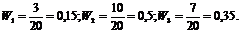
Напишем распределение относительных частот:
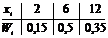
Контроль: 
Пусть имеется вариационный ряд 
,где 
. Найдем эмпирическую функцию распределения.
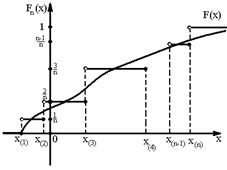
Если n велико, то 
, где F(x) – функция распределения генеральной совокупности.
Таким образом, эмпирическая функция распределения служит для оценки функции распределения генеральной совокупности.
Пример 2 Построить эмпирическую функцию распределения по данному распределению выборки:
Решение Найдем объем выборки 12+18+30=60. Наименьшая варианта равна 2, следовательно:
при 
.
Значение 
наблюдалось 12 раз, следовательно
при 
.
Значение 
, а именно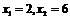 
наблюдалось 12+18=30 раз, следовательно,
при 
.
Так как x=10 – наибольшая варианта, то
при 
.
Искомая эмпирическая функция:
График этой функции:
Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.
О. Полигоном частот называют ломаную, отрезки которой соединяют точки 
Для построения полигона частот на оси абсцисс откладывают варианты 
, а на оси ординат – соответствующие им частоты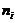 
. Точки 
соединяют отрезками и получают полигон частот.
О. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 
Предположим, что 
- выборка из непрерывной генеральной совокупности с плотностью вероятности 
. Необходимо построить оценку плотности 
.
Интервал, в котором заключены все наблюдаемые значения, разбиваем на k частичных интервалов длины
, где 
- наибольшая, а 
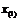- наименьшая из вариант,
, где 
- число выборочных значений, попадающих в i – й интервал 
, n – объем выборки.
Полученная ступенчатая фигура называется гистограммой относительных частот.
О. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной 
, а высоты равны отношению 
(вместо 
).
Площадь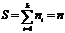 
, т.е. равна сумме всех частот, т.е. объему выборки.
2.1.3 Определение распределения Гаусса и его свойства. РАСПРЕДЕЛЕНИЕ ХИ - КВАДРАТ.
Пусть Xi, 
—нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)—единице. Тогда сумма квадратов этих величин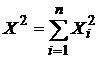 
распределена по закону Х2 с k=n степенями свободы. Если же эти величины Хi связаны одним линейным соотношением, например 
, то число степеней свободы k=n-1.
Плотность этого распределения 
, где 
—гамма-функция; в частности, Г(n+1)=n!
Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
Распределение Стьюдента.
Пусть Z—нормально распределенная величина, причем M(Z)=0, G2=1, т.е. Z~N(0,1), а V—независимая от Z величина, которая распределена по закону Х2 с k степенями свободы. Тогда величина 
имеет распределение, которое называют t—распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.
Плотность распределения случайной величины t имеет вид 
, 
.
Случайная величина t имеет математическое ожидание Mt=0, 
(k>2).
Распределение Фишера.
Если U и V—независимые случайные величины, распределенные по закону Х2 со степенями свободы k1 и k2, то величина 
имеет распределение Фишера F со степенями свободы k1 и k2. Плотность этого распределения 
, где
.
Распределение Фишера F определяется двумя параметрами—числами степеней свободы.
