o Случайной функцией называется функция X(t), значение которой при любом значении аргумента t является случайной величиной.
Другими словами, случайной функцией называется функция, которая в результате опыта может принять тот или иной конкретный вид, при этом заранее не известно, какой именно.
o Конкретный вид, принимаемый случайной величиной в результате опыта, называется реализацией случайной функции.
o 
Т.к. на практике аргумент t чаще всего является временным, то случайную функцию иначе называют случайным процессом.
o На рисунке изображено несколько реализаций некоторого случайного процесса.
o Если зафиксировать значение аргумента t, то случайная функция X(t) превратится в случайную величину, которую называют сечением случайной функции, соответствующим моменту времени t. Будем считать распределение сечения непрерывным. Тогда Х(t) при данном t определяется плотностью распределения p(x; t).
o Очевидно, p(x; t) не является исчерпывающей характеристикой случайной функции X(t), поскольку она не выражает зависимости между сечениями X(t) в разные моменты времени t. Более полную характеристику дает функция 
—совместная плотность распределения системы случайных величин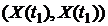 
, где t1 и t2—произвольные значения аргумента t случайной функции. Еще более полную характеристику случайной функции X(t) даст совместимая плотность распределения системы трех случайных величин 
и т.д.
o Говорят, что случайный процесс имеет порядок n, если он полностью определяется плотностью совместимого распределения 
n произвольных сечений процесса, т.е. системы n случайных величин 
, где X(ti)—сечение процесса, отвечающее моменту времени ti, но не определяется заданием совместного распределения меньшего, чем n, числа сечений.
o Если плотность совместного распределения произвольных двух сечений процесса вполне его определяет, то такой процесс называется марковским.
Пусть имеется случайная функция X(t). Возникает задача описания ее с помощью одной или нескольких неслучайных характеристик. В качестве первой из них естественно взять функцию 
— математическое ожидание случайного процесса. В качестве второй берется среднее квадратическое отклонение случайного процесса 
.
Эти характеристики являются некоторыми функциями от t. Первая из них— это средняя траектория для всех возможных реализаций. Вторая характеризует возможный разброс реализаций случайной функции около средней траектории. Но и этих характеристик недостаточно. Важно знать зависимость величин X(t1) и X(t2). Эту зависимость можно характеризовать с помощью корреляционной функции или корреляционного момента.
. 
Пусть имеются два случайных процесса, по нескольку реализаций которых изображено на рисунках.
У этих случайных процессов примерно одинаковые математические ожидания и средние квадратичные отклонения. Тем не менее это различные процессы. Всякая реализация для случайной функции X1(t) медленно меняет свои значения с изменением t, чего нельзя сказать о случайной функции X2(t). У первого процесса зависимость между сечениями X1(t) и 
будет больше, чем зависимость для сечений X2(t) и 
второго процесса, т.е. 
убывает медленнее, чем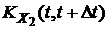 
, при увеличении Δt. Во втором случае процесс быстрее «забывает» свое прошлое.
Остановимся на свойствах корреляционной функции, которые вытекают из свойств корреляционного момента пары случайных величин.
Свойство 1. Свойство симметричности 
.
Свойство 2. Если к случайной функции X(t) прибавить неслучайное слагаемое 
, то от этого корреляционная функция 
не изменится, т.е. 
.
Действительно, 
Свойство 3. 
, где —неслучайная функция.
При 
o Центрированной случайной функцией 
, соответствующей X(t), называется 
(2)
Очевидно, математическое ожидание центрированной функции—тождественный нуль, среднее квадратичное отклонение и корреляционная функция такие же, как и у X(t).
o Нормированной называется случайная функция
(3),
, 
.
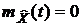Для этой функции 
, , 
—коэффициент линейной корреляции между X(t1) и X(t2).
