2.5.1 Понятие функции правдоподобия для дискретных случайных величин.
2.5.2 Понятие функции правдоподобия для непрерывных случайных величин.
2.5.3 Сущность метода максимального правдоподобия.
Понятие функции правдоподобия для дискретных случайных величин.
Пусть 
выборка из генеральной совокупности, имеющей плотность 
, зависящую от 
. Составим совместную плотность распределения случайных величин .
(по критерию независимости непрерывных случайных величин)= 
. 
- функция правдоподобия.
Понятие функции правдоподобия для непрерывных случайных величин.
Фишер предложил находить оценки 
из того условия, что функция правдоподобия 
.
Те значения , при которых функция 
принимает наибольшее значение, и являются оценками.
Введем функцию 
- логарифмическую функцию правдоподобия. Надо решать задачу 
.
Для этого составляется система
Выбирается то решение, которое обращает функцию правдоподобия (следовательно, и 
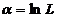) в максимум. При этом методе получаются состоятельные,но смещенные оценки.
2.5.3 Сущность метода максимального правдоподобия. Пример. Имеется выборка из ГС с 
. Найти оценки 
и 
.
;
;
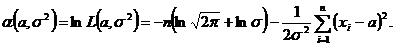
Составим систему:
Тема2.6Регрессионныйанализ 2.6.1 Задачи регрессионного анализа.
2.6.2 Линейная регрессия.
2.6.3Средняя квадратическая ошибка оценок регрессии. 2.6.1 Задачи регрессионного анализа
Основная теорема регрессионного анализа.
Теорема (Основная теорема регрессионного анализа).
Наилучшим прогнозом случайной величины Y по случайной величине X в среднем квадратическом смысле является условное математическое ожидание 
. Другими словами, если h(x) – любой прогноз Y по X, то математическое ожидание 
Линейная регрессия
О. Уравнение Y=f(X), где f(X)=M[Y|X], называется уравнением регрессии Y на X (прогноза Y по X).
Если обозначить через g(Y)=M(X|Y), то
О. Уравнение X=g(Y), где g(Y)=M(X|Y) называется уравнением регрессии X на Y (гипотеза Y по X)
О. Регрессия Y на X называется линейной, если f(X)=M(Y|X)=a0+a1X. (1)
О. Регрессия X на Y называется линейной, если g(Y)=M(X|Y)=b0+b1Y.
Обозначим через MX=a, MY=b,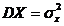 
, 
и через r коэффициент корреляции 
Применим математическое ожидание к обеим частям уравнения (1) 
Вычтем из (1)-(2’)
Применим операцию МО еще раз
Из этого находим постоянную 
. Подставим в (3) 
.
Искомое уравнение регрессии имеет вид: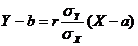 
- уравнение линейной регрессии Y на X. Аналогично 
- уравнение линейной регрессии X на Y.
Линии регрессии:
, 
Коэффициент корреляции:
r‹0 ó 
<0, 
<0;
r>0ó >0, >0.
Таким образом,
r<0 ó 
и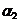 
– тупые углы;
r>0 ó и 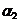– острые углы.
Линии регрессии совпадут ó = ó 
ó 
ó 
.
Чем меньше угол β, тем точнее прогноз, который даёт линейная регрессия.
Выборочные уравнения линейной регрессии.
На практике, как правило, иметься только выборка. Например, (
),…,(
).
Эмпирический коэффициент корреляции r является мерой тесноты линейной связи между двумя случайными величинами. С геометрической точки зрения это означает, что чем теснее располагаются точки на диаграмме рассеивания вокруг линии регрессии, тем выше абсолютная величина регрессии и наоборот. На рисунке 1-4 изображены несколько диаграмм рассеивания.
рис.1
| 
рис.2
|
рис.3
| 
рис.4
|
Диаграмма на рис.1 указывает на отрицательную функциональную связь
(r=-1), на рис.2- на относительно высокую степень положительной корреляции (r≈0,8), на рис.3- умеренную степень отрицательной корреляции (r≈ -0,5), на рис.4 – отсутствие корреляции (r=0). По диаграмме рис.4 видно, что если коэффициент корреляции равен 0, то независимо от того, чему равна величина переменной X, оцениваемая величина зависимой переменной всегда равна 
.
Сначала для построения диаграммы рассеивания строят корреляционное поле, т.е. наносят на плоскость все точки.
рис.5
| Если видят, что точки имеют тенденцию к линейной зависимости, начинают строить линейную регрессию. |
рис.6
| Если же точки расположены как на рис.6, то строят параболическую регрессию и уравнение вида параболы. |
Обозначим а=МХ, в=МУ, 
=DX, 
=DY, r= 
. Т.к. наши параметры неизвестны, то вместо них логично взять их оценки: 
, 
; 
;
cov(X,Y)=M[(X-MX)(Y-MY)]; cov(X,Y)≈ 
.Коэффициент корреляции r= 
Подставляя в уравнение линейной регрессии оценки, получаем:
-выборочное уравнение линейной регрессии Y на X.
- выборочное уравнение линейной регрессии X на Y.
