o Процесс X(t) называется стационарным в узком смысле, если плотность его распределения 
удовлетворяет условию 
(1) для 
. Если (1) выполняется для n=2, то случайный процесс называется стационарным в широком смысле.
Для стационарных процессов
.
Аналогично можно показать, что 
также не зависит от времени t. Переходим к нахождению корреляционной функции случайного процесса:
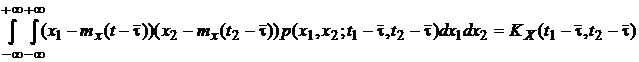
o Процесс X(t) называется стационарным в узком смысле, если плотность его распределения удовлетворяет условию (1) для . Если (1) выполняется для n=2, то случайный процесс называется стационарным в широком смысле.
Для стационарных процессов
.
Аналогично можно показать, что также не зависит от времени t. Переходим к нахождению корреляционной функции случайного процесса:
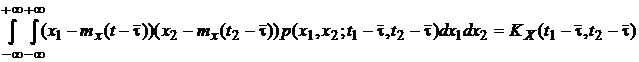
o Положим 
, тогда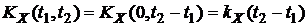 
зависит от разности 
. Положим 
. Тогда имеем 
. Т.к.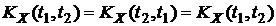 
, то корреляционная функция 
четная.
o На рисунке изображен график корреляционной функции одного из стационарных процессов.
| o o |
o Пусть X(t)—стационарный случайный процесс. Его корреляционная функция 
— четная функция от τ. Например, если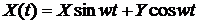 
, где X и Y—некоррелированные случайные величины, у которых 
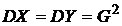, то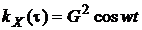 
.
o Теорема. Если X(t) и Y(t)—некоррелированные стационарные случайные функции, то их сумма 
— также стационарная функция.
o 
o 
,
o 
. 
.
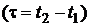Раздел 2 Математическая статистика
Тема 2.1 Распределения Гаусса, Пирсона, Фишера, Стьюдента
2.1.1 Основы выборочного метода.
2.1.2 Эмпирическая функция распределения.
2.1.3 Определение распределения Гаусса и его свойства.
Основы выборочного метода
Задачи математической статистики.
Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных – результатов наблюдений.
Математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирования эксперимента); в ходе исследования (последовательный анализ) и решает многие другие задачи.
Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача МС - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
в) установление статистических зависимостей между случайными событиями, случайными величинами или случайными процессами (регрессионный, корреляционный, дисперсионный, дискриминантный анализ);
г) управление случайными процессами;
д) планирование эксперимента.
Математическая статистика возникла в ХV11 веке и развивалась параллельно с ТВ. Дальнейшее развитие МС обязано таким видным ученым Х1Х – ХХ вв. как Чебышев П.Л., Марков А.А., Ляпунов А.М., Гаусс К., Кетле А., Дальтон Ф., Пирсон К., Стьюдент, Колмогоров А.Н., Смирнов Н.В., Нейман Ю., А.Вальд.
О. МС – наука о способах получения, сокращения, хранения и обработки информации.
В теории вероятностей по вероятностям некоторых событий находятся вероятности более сложных событий, связанных с первоначальными. По законам распределения одних случайных величин находятся законы распределения сложных СВ, зависящих от первоначальных.
Пример: Имеется с.в. 
~ 
. Найти закон распределения случайной величины 
.
Математическая статистика позволяет получить оценку первоначальных вероятностей. Пусть Р(А)=р; N – общее число испытаний, N(A) – число испытаний, в которых появилось событие А. Относительная частота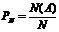 
появления события А 
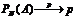(сходится по вероятности). 
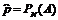- оценка величины р при 
.
Генеральная совокупность. Выборка.
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали.
Иногда проводят сплошное обследование, т.е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование нет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.
О. Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
О. Генеральной совокупностью называется совокупность объектов, из которых производится выборка.
О. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100.
Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако, если это число достаточно велико, то иногда в целях упрощения вычислений или для облегчения теоретических выводов, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки.
Для того чтобы по данным выборки можно было достаточно уверено судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируется так:
выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.
Предположим, что можем производить измерения случайной величины Х. Допустим, что в n экспериментах результаты измерений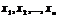 
- некоторые числа.
Предполагаем, что выполняются следующие две предпосылки:
Эксперименты проводятся в одинаковых условиях;
Эксперимента проводятся независимо друг от друга.
О. Говорят, что результаты n экспериментов 
образуют конкретную выборку объема n из генеральной совокупности случайной величины Х, если выполняются предпосылки 1 и 2. Величину Х называют теоретической случайной величиной.
Пусть требуется произвести измерения случайных величин 
. Если производить измерения сериями, то результаты можно записать следующим образом:
- 1 серия;
- 2 серия;
… …. ….
- к-ая серия;
… … … …
Тогда случайные величины 
- абстрактные результаты измерений (т.е. результаты экспериментов до того, как мы их проверили).
Если 
, то можно представить себе бесконечную генеральную совокупность. Тогда Х – непрерывная СВ.
Из первой предпосылки следует, что - одинаково распределенные случайные величины, имеющие один и тот же закон распределения, совпадающий с законом распределения случайной величины Х.
Из второй предпосылки следует, что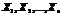 
- независимые случайные величины.
О. Говорят, что случайные величины образуют абстрактную выборку объема n, если они независимы и одинаково распределены.
О. Функция распределения F(x) случайной величины Х называется теоретической функцией распределения или функцией распределения генеральной совокупности.
Как абстрактную, так и конкретную выборку будем обозначать одними и теми же буквами 
и называть выборкой.
При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные.
О. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
О. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида:
Отбор, не требующий разбиения (расчленения) генеральной совокупности на части. Сюда относятся:
а) простой случайный бесповторный отбор;
б) простой случайный повторный отбор.
Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся:
а) типический отбор;
б) механический отбор;
в) серийный отбор.
О. Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности.
Осуществить простой отбор можно различными способами. Например, для извлечения n объектов из генеральной совокупности объема N поступают так: выписывают номера от 1 до N на карточках, которые тщательно перемешивают, и наугад вынимают карточку; объект, имеющий номер, указанный на карточке, подвергают обследованию. Затем карточки перемешивают, наугад вынимают одну из них и т.д. Так поступают n раз. В итоге получают простую случайную повторную выборку объема n.
Если извлеченные карточки не возвращать в пачку, то выборка является простой случайной бесповторной.
При большом объеме генеральной совокупности описанный процесс является очень трудоемким. В этом случае пользуются готовыми таблицами “случайных чисел”, в которых числа расположены в случайном порядке.
О. Типическим называют отбор, при котором объекты выбираются не из всей генеральной совокупности, а из каждой ее “типической” части.
Например, если детали изготовлены на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности.
Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если продукция изготовлена на нескольких станках, среди которых есть более и менее изношенные, то в данном случае типический отбор целесообразен.
О. Механическим называют отбор, при котором генеральную совокупность “механически” делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Например, если нужно отобрать 20% изготовленных деталей, то отбирают каждую пятую деталь.
Замечание: Необходимо отметить, что иногда механический отбор может не обеспечить репрезентативность выборки. Например, если замена резца в станке проводится сразу после отбора каждой двадцатой детали, то обратными окажутся все детали, обточенные затупленными резцами. В таком случае можно устранить совпадение ритма отбора с ритмом замены резца.
О. Серийным называют отбор, при котором объекты отбираются из генеральной совокупности не по одному, а “сериями”, которые подвергаются сплошному обследованию.
Например, если изделия изготовлены большой группой станков, то подвергают сплошному обследованию только продукцию нескольких станков. Серийным отборам пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно.
На практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы. Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором отбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.
