2.3.1 Основные понятия теории проверки гипотез.
2.3.2 Проверка гипотез о числовых значениях.
2.3.3 Проверка гипотез о равенстве средних.
Основные понятия теории проверки гипотез
Проверка статистических гипотез.
Предположим, что x1,…,xn – выборка из генеральной совокупности с функцией распределения F(x). F(x) может быть полностью неизвестна, тогда можно поставить следующую гипотезу:
H0: F(x)=F0(x), где F0(x) – конкретная функция распределения. Если вид функции распределения 
известен с точностью до каких-то m неизвестных параметров. Тогда гипотеза 
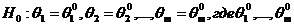- заданные числа. Пусть x1,…,xn - берется из нормальной генеральной совокупности.
Допустим 
-известно и оно равно 1, т.е. ГС ~ N(a,1). Тогда 
или 
.
Пусть известно a=0, т.е. выборка берется из 
. 
или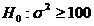 
.
Пусть a и 
неизвестны: 
или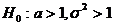 
Подчеркнутые гипотезы называются простыми, поскольку задают единственную точку в пространстве параметров. Если гипотеза задает 2 и большее число точек в пространстве, то такая гипотеза называется сложной.
H0 – основная или нулевая гипотеза.
H1 – конкурирующая гипотеза или альтернатива.
Пример: Пусть x1,x2,…,xn – выборка из нормальной генеральной совокупности с параметрами 
или или и т.д
Мы будем предполагать, что одна из H0 или H1 обязательно верна.
Пусть X- выборочное пространство, т.е. это множество возможных значений вектора 
. Для построения критерия проверки гипотезы в выборочном пространстве выбирается критическая область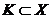 
таким образом, что если 
, то нулевая гипотеза H0 отвергается, т.е. принимается гипотеза H1, а если 
не попадает в область K, т.е. 
, то H0 – принимается.
Обычно K выбирается следующим образом:
D=D(x1,x2,…,xn) - некоторая функция от выборочных ранных значений, т.е. случайная величина.
Обычно критическая область K выбирается одним из следующих 3-х способов: 
односторонние критические области
двусторонняя критическая область
| 1. |
| Правосторонняя критическая область |
| 2. | 
| Левосторонняя критическая область |
| 3. | 
| Двусторонняя критическая область |
Чаще всего двусторонняя область строится в виде: 
|
|
О. Случайная величина D=D(x1,x2,…,xn) называется статистикой критерия.
Ошибки:
Ошибка 1-го рода возникает, если H0 – отвергается при условии, что H0 – верна.
-вероятность ошибки 1-го рода. 
.
О. Вероятность ошибки 1-го рода называется уровнем значимости критерия.
Ошибка 2-го рода возникает тогда, когда H0 принимается, хотя она неверна (т.е. верна H1).
-вероятность ошибки 2-го рода. 
.
Одновременно 
невозможно. Если увеличивать, то будет уменьшаться и наоборот.
Классическая постановка задачи заключается в следующем: 
- фиксированное ( =0,01, =0,05) так чтобы 
и при этом условии K выбирают из того условия, чтобы была как можно меньше.
Чаще всего на практике выдвигается H0, а H1 не выдвигается, и задают уровень значимости =0,05; 0,01; 0,005; 0,001.
задают таким образом, чтобы событие, имеющее вероятность было практически невозможно. Поэтому находится K, исходя из условия, что .
Если , то произошло событие с вероятностью , значит, H0 отвергается.
Если , то произошло событие с вероятностью 1- , значит H0 согласуется с экспериментальными данными.
О. Все критерии, построенные на таком принципе, называются критериями значимости.
Предположим, что имеется выборка x1,x2,…,xn из генеральной совокупности с неизвестной функцией распределения F(x). Предположим, что имеется гипотеза H0 : F(x)=F0(x), где F0(x) – заданная функция распределения.
