1.6.1 Неравенство Чебышева.
1.6.2 Сходимость последовательности случайных величин.
1.6.3 Теорема Маркова.
1.6.4 Теорема Бернулли.
Неравенство Чебышева.
Законы больших чисел.
0. 1 Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа 
, т.е. 
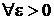
при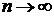 
. Обозначается 
.
0.2 Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если 
.
Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство Чебышёва:
Для .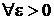 
.
{x││x-MX│≥ε}
{x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε}
.
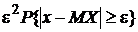Таким образом, 
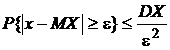. 1.6.2 Сходимость последовательности случайных величин.
Теорема 2. (закон больших чисел в форме Чебышёва).
Пусть Х1,Х2,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е.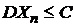 
. Тогда эта последовательность удовлетворяет закону больших чисел.
Обозначим через 
. Нужно доказать, что 
.
.
Отсюда 
(т.к. 
).
1.6.4 Теорема Бернулли.
Теорема 3. (Закон больших чисел в форме Бернулли).
Пусть μ—число успехов в n независимых испытаниях Бернулли с вероятностью успеха р в одном испытании, тогда 
.
Введем случайные величины μi—число успехов в i-ом испытании. Тогда 
.
| μi | 1 | 0 |
| P | p | q |
, 
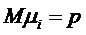(т.к. 
).
(т.е. дисперсия ограничена 
).
μ1, μ2,…, μn—независимы. По закону больших чисел в форме Чебышёва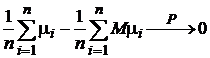 
.
.
.
В чем смысл закона больших чисел в форме Бернулли?
Пусть в результате эксперимента может произойти или не произойти событие А. P(A)—вероятность события А в одном эксперименте. Эксперимент повторяется N раз, N(A)—число появлений события А в этих N экспериментах.
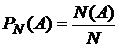—относительная частота появления события А.
. N(A)=μ, 
.
Таким образом, закон больших чисел в форме Бернулли теоретически подтверждает устойчивость относительных частот, т.е. стабилизацию при большом числе испытаний относительной частоты вокруг вероятности (относительная частота ≈ Р(А)).
Тема 1.7 Характеристическая функция
1.7.1 Производящие функции
1.7.2 Понятие характеристической функции
1.7.3 Свойства характеристических функций.
Производящие функции.
o Под целочисленной случайной величиной будем понимать дискретную случайную величину, которая может принимать значения 0,1,2,…
Таким образом, если случайная величина Х—целочисленная, то она имеет ряд распределения
| Х | 0 | 1 | 2 | … |
| Р | р0 | р1 | р2 | … |
o Пусть Х—целочисленная величина с законом распределения
| Х | 0 | 1 | 2 | … |
| Р | р0 | р1 | р2 | … |
Ее производящей функцией называется функция 
