Формула свертки. Устойчивость нормального распределения.

o Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y:

       .

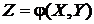Далее на примерах будет показано, как найти распределение функции  по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если Х—погрешность показаний измерительного прибора (распределена равномерно),  то   возникает задача —  найти  закон   распределения  суммы погрешностей .

Случай 1. Пусть Х и Y— дискретные независимые случайные величины. Для того чтобы составить закон распределения функции Z=X+Y, надо найти все возможные значения Z и их вероятности. Иными словами, составляется ряд распределения случайной величины Z.

Пример 1. Дискретные независимые случайные величины Х и Y, заданы распределениями

Х	1	2
Р	0,4	0,6

и

Y	3	4
P	0,2	0,8

Составить распределение случайной величины Z=X+Y.

Возможные значения Z есть суммы каждого возможного значения Х со всеми возможными значениями Х.

; ; ; .

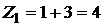Найдем вероятность этих возможных значений. Для того чтобы Z=4 достаточно, чтобы величина Х приняла значения х₁=1 и величина Y—значение y₁=3. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равно 0,4 и 0,2.

Поскольку случайные величины Х и Y независимы, то события Х=1 и Y=3 независимы и, следовательно, вероятность их совместного наступления (т.е вероятность события Z=1+3=4) по теореме умножения равна 0,4·0,2=0,08.

Аналогично найдем

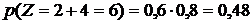
Напишем искомое распределение, сложив предварительно вероятности несовместимых событий Z=z₂ и Z=z₃. (0,32+0,12=0,44)

Z	4	5	6
P	0,08	0,44	0,48

Контроль: 0,08+0,44+0,48=1.

Рассмотрим общий случай:

Пусть Х и Y—независимые случайные величины, принимающие значения . Обозначим через , , .

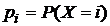
Z=X+Н. Обозначим через

.

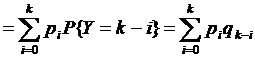       Таким образом, — формула свертки.

Случай 2. Пусть Х и Y—непрерывные случайные величины.

Теорема. Если Х и Y—независимые непрерывные случайные величины, то случайная величина Z=X+Y—также непрерывна, причем плотность распределения случайной величины Z —формула свертки.

o Плотность распределения суммы независимых случайных величин называется композицией.

Замечание. Если возможные значения X и Y неотрицательны, то формула свертки .

o Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон распределения (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойствами устойчивости, т.е. композиция нормальных законов также имеет нормальное распределение, причем математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых:

, .

В частности, если Х~N(0,1) и Y~N(0,1), то Z=X+Y~N(0,2).

Пример 2. Пусть случайная величины Х₁,…,Х_k—независимы и имеют показательное распределение с параметром λ>0, т.е. .

. Найти плотность распределения .

Если x>0

.

Если x≤0, то . Таким образом,

.

Далее при x>0

.

Если x≤0, то .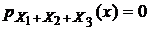

Проводя аналогичные рассуждения, получим:

.

 Числовые характеристики системы

Двух случайных величин.

 

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий используют и другие характеристики. К их числу относятся ковариация и коэффициент коррекции.

o Ковариацией между случайными величинами Х и Y называется число , где .

Для непрерывных случайных величин X и Y используют формулу .

Покажем, что если случайные величины Х и Y независимы, то . Пусть Х и Y—непрерывные случайные величины

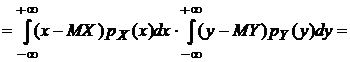
o Коэффициентом корреляции между случайными величинами Х и Y называется число .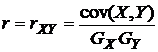

Свойства корреляции.

Свойство 1. Абсолютная величина коэффициента корреляции не превосходит единицы, т.е. .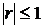

Свойство 2. Для того чтобы  необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е.  с вероятностью 1.

Свойство 3. Если случайные величины независимы, то они некоррелированы, т.е. r=0.

Пусть Х и Y—независимы, тогда по свойству математического ожидания

o Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля.

o Случайные величины Х и Y называют некоррелированными если их коэффициент корреляции равен 0.

Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

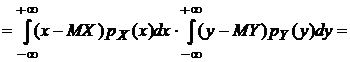
o Коэффициентом корреляции между случайными величинами Х и Y называется число .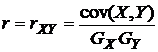

Свойства корреляции.

Свойство 1. Абсолютная величина коэффициента корреляции не превосходит единицы, т.е. .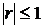

Свойство 2. Для того чтобы  необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е.  с вероятностью 1.

Свойство 3. Если случайные величины независимы, то они некоррелированы, т.е. r=0.

Пусть Х и Y—независимы, тогда по свойству математического ожидания

o Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля.

o Случайные величины Х и Y называют не коррелированными если их коэффициент корреляции равен 0.

Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости.

o Коэффициентом асимметрии случайной величины Х называется число

 

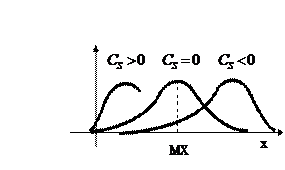Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.

 

o Эксцессом случайной величины Х называется число .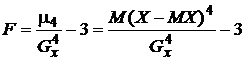

Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.