О2. Оценка 
неизвестного параметра 
называется несмещенной, если математическое ожидание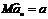 
. О3. Оценка 
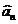неизвестного параметра 
называется состоятельной, если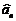 
сходится по вероятности к
(т.е. для 
) 
.
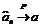О4. Несмещенная оценка 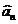неизвестного параметра называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок параметра .
┐ 
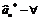
несмещенная оценка параметра , тогда 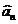эффективна, если 
Пример: Предположим, что имеется выборка 
из генеральной совокупности с 
, 
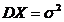. Здесь - генеральная средняя, 
- генеральная дисперсия.
В качестве оценки возьмем выборочную среднюю 
. В качестве оценки возьмем выборочную дисперсию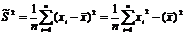 
. Проверим, насколько хороша оценка 
:
1. 
.
Вывод: - несмещенная оценка параметра .
2. Поскольку 
- независимы, 
. По закону больших чисел в форме Чебышева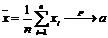 
.
По определению 3 - состоятельная оценка параметра .
3. Эффективность оценки зависит от закона распределения генеральной совокупности.
Оценка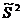 
.
1. 
.
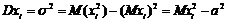Следовательно, 
(1)
.
.
Следовательно, 
(2)
Следовательно,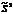 
не является несмещенной оценкой. При 
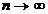оценка 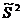будет почти несмещенной.
2. Можно проверить, что 
- состоятельная. Введем 
, тогда
.
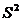- несмещенная оценка и называется исправленной выборочной дисперсией.
- неисправленная выборочная дисперсия.
- исправленная выборочная дисперсия.
Пусть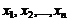 
- выборка из генеральной совокупности с функцией распределения 
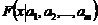, зависящей от 
неизвестных параметров. Необходимо найти оценки 
параметров 
.
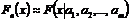при больших 
.
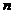Более того, можно рассматривать 
как оценку 
или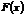 
при каждом фиксированном значении 
.
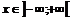Поскольку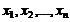 
- результаты n испытаний для случайной величины 
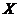, то в качестве успеха в случайном испытании примем:
.
Тогда 
, где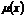 
- число выборочных значений, меньших 
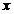, т.е. число успехов.
, где 
,
.
Таким образом, 
.
Следовательно,
1. 
.
При любом фиксированном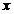 
является несмещенной оценкой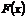 
.
2. Проверим состоятельность оценки 
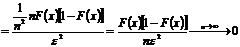т.к.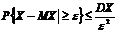 
,
если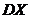 
- конечно.
По теореме о двух милиционерах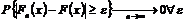 
.
Т.о. 
, т.е.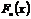 
- состоятельная оценка .
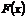3. Оказывается, что эта оценка является также и эффективной.
2.2.3 Понятие точечной оценки параметра. Интервальные оценки неизвестных параметров.
Пусть имеется выборка 
объема n из генеральной совокупности, функция распределения которой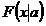 
зависит от неизвестного параметра . Полученная точечная оценка неизвестного параметра не позволяет непосредственно ответить на вопрос, какую ошибку мы совершаем, принимая вместо точного значения неизвестного параметра некоторое его приближенное значение (оценку)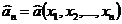 
. В связи с этим во многих случаях более выгодно пользоваться интервальной оценкой, основанной на определении некоторого интервала, внутри которого с определенной вероятностью находится неизвестное значение параметра .
Пусть имеется точечная оценка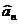 
неизвестного параметра . Чем меньше 
, тем лучше качество оценки. Таким образом, положительное число 
такое что 
(характеризует точность оценки).
Для построения интервальных оценок американский статистик Ю.Нейман разработал метод доверительных интервалов, который базируется на идеях английского статистика Р.Фишера.
О. Случайные величины н= н() и 
, являющиеся функциями от выборочных значений, называются соответственно нижним и верхним двусторонними доверительными пределами для неизвестного параметра с надежностью (коэффициентом доверия, доверительной вероятностью) P (0,5<P<1) (или с уровнем значимости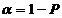 
), если для доверительного интервала вероятность 
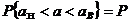. (1)
При этом интервал 
называется двусторонним доверительным интервалом для параметра .
Замечание 1. Надежность P=0,9; 0,95; 0,99 выбирается близкой к единице, а 
=0,1; 0,05; 0,01 – уровень значимости. Параметр лежит в пределах 
.
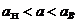Замечание 2. В соотношение (1) случайными являются 
и 
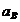, - число.
Замечание 3. Пусть 
- точечная оценка параметра . Если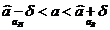 
- доверительный интервал. Тогда - точность интервальной оценки.
Пример: Предположим, что - выборка из нормального распределения генеральной совокупности с параметрами 
. Построить доверительные интервалы для и . Могут возникнуть 4 случая:
Пусть - известно. Построить ДИ для . Этот ДИ нужно строить при помощи точечной оценки . По следствию из теоремы 1.
~N(
).
По лемме о нормальном распределении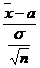 
~N(0,1). Поэтому 
.
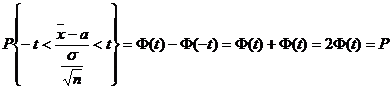- функция Лапласа.
t – корень уравнения 
.
Решим левое неравенство относительно :
.
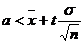Решим правое неравенство относительно :
.
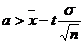Следовательно, получаем:
,
где 
- точность оценки.
Пусть - неизвестно. Надо построить ДИ для .
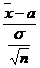~N(0,1).
С другой стороны, по лемме Фишера:
.
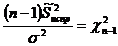Отсюда 
.
- отношение Стьюдента с n-1 степенью свободы.
.
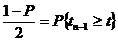Здесь 
, где 
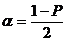- уровень значимости для процентных точек.
- искомый ДИ.
Пусть - известно. Построить интервальную оценку для .
- неисправленная выборочная дисперсия.
По лемме Т1. 
. Поэтому вероятность того, что
, 
.
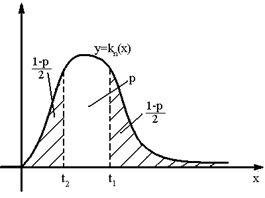
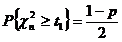, где 
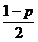- уровень значимости.
.
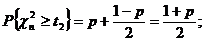
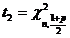- искомый ДИ.
4. Пусть - неизвестно. Построить ДИ для .
.
По Лемме Фишера 
.
;
, 
, 
.
, 
.
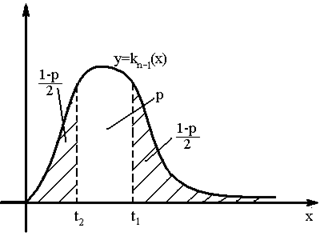
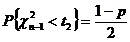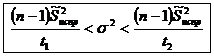- искомый ДИ.
