Критерии согласия.
Предположим, что имеется выборка x1,…,xn объема n из генеральной совокупности с неизвестной функцией распределения F(x). H0: F(x)=F0(x), где F0(x) – заданный закон распределения (функция распределения).
Гипотеза такого вида называется гипотезой согласия, а критерий для проверки гипотезы согласия называется критерием согласия.
Критерий согласия 
- Пирсона.
В критерии - Пирсона в качестве меры отклонения теоретической функции распределения F(x) от эмпирической функции распределения Fn(x) выбирается величина 
Обозначим через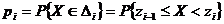 
, 
- число выборочных значений, попавших в интервал 
, 
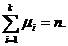2.4.2 Критерий существования достаточной статистики.
Минимальные достаточные статистики.
Теорема (Пирсона).
Пусть , тогда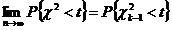 
, где случайная величина 
имеет распределение с (k-1) степенью свободы. 
, тогда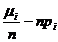 
- мало 
– небольшое число. Если предположим, что H0 – верна, то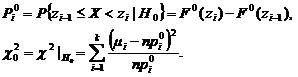 
.
Задаем уровень значимости 
. 
, 
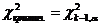(% точка распределения X2).
Если 
гипотеза H0 отвергается. Если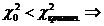 
H0 согласуется с экспериментальными данными.
Алгоритм следующий:
Разбиваем всю числовую ось на k интервалов (отрезков).
Находим .
Производим расчет вероятностей
Рассчитываем 
По таблице процентных точек распределения находим критическое: 
Проверяем: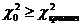 
- H0 – отвергается; 
- H0– согласуется с экспериментальными данными.
Замечание: Пусть закон распределения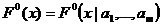 
зависит от m неизвестных параметров. Тогда эти параметры заменить их оценками 
и проверить нулевою гипотезу в виде: 
. Тогда оказывается, что теорема Пирсона будет верна с некоторыми поправками и примет вид: 
. Поэтому предварительно находятся оценки параметров и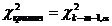 
.
Минимальные достаточные статистики.
Критерий 
Мизиса -Смирнова.
Пусть x1,…,xn – выборка из генеральной совокупности с неизвестной функцией распределения F(x). Проверить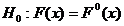 
.
В качестве меры отклонения теоретической функции от эмпирической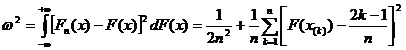 
, где 
-k-ый член вариационного ряда 
, т.е. 
. Обозначим через 
.
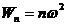Теорема (Смирнова). Если функция распределения F(x) непрерывна, то 
, который не зависит от вида функции распределения F(x).
Без доказательства.
Имеются таблицы процентных точек, позволяющие находить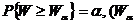 
-% точка).
Находим 
Находим 
по таблице.
Если 
, то H0 отвергается.
Если 
, то H0 согласуется с экспериментальными данными.
Критерий Колмогорова.
Имеется выборка x1,…,xn и H0: F(x)=F0(x). В качестве меры отклонения теоретической функции распределения F(x) берется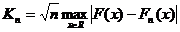 
.
Теорема (Колмогорова).
Если F(x) непрерывна, то 
. Имеются таблицы процентных точек распределения Колмогорова.
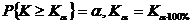- процентная точка распределения Колмогорова, соответствующая уровню значимости или 
.
Алгоритм:
Считаем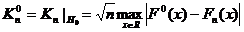 
.
Если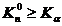 
, то H0 отвергается.
Если 
, то H0 согласуется с экспериментальными данными.
