Теорема. Интеграл с переменным верхним пределом равен первообразной функции f(x). Если функция f (x) непрерывна на интервале [a,b], то функция
Ф(х) = 
где 
, дифференцируема в любой внутренней точке х этого интервала, причем Ф¢(x) = f (x), то есть функция Ф(х) является первообразной функции f (x). Функция Ф(х) называется интегралом с переменным верхним пределом.
Доказательство. Найдем производную функции Ф(x). Для этого вначале выберем приращение аргумента D х столь малым, чтобы точка х + D х лежала внутри отрезка [ a,b ], и найдем приращение функции Ф(х) (рис. 5.5, приращение обозначено зеленым цветом).
DФ(х) = Ф(х + D х) - Ф(х) = 
=
Здесь мы использовали свойство аддитивности. К полученному интегралу применим теорему о среднем (5.13)
DФ(x) = 
= f (с)D x, где с Î [ x, x +D x ].
Рис. 5.5. Интеграл с переменным верхним пределом.
Следовательно, 
= f (с). Поскольку f (x) непрерывна и, если D х ® 0, то с ® x, а 
Поэтому производная функции Ф(х) равна f (x)
. (5.13)
А так как производная функции Ф(х) равна f (x), то, по определению первообразной, Ф(х) первообразная. Следовательно, интеграл от функции f (x) с постоянным нижним и переменным верхним пределом х, есть одна из первообразных функции f (x) 
.
Теорема. Формула Ньютона – Лейбница. Если функция f (x) непрерывна на интервале [ a,b ], то определенный интеграл равен разности значений первообразной 
на концах промежутка
. (5.14)
Доказательство. В силу непрерывности на отрезке [ a,b ] функция f (x) интегрируема и, на основании предыдущей теоремы, имеет первообразную
Ф(x) = 
= F (x) + C. (5.15)
Константу С легко выразить через значение первообразной F (х) в точке а. Действительно, принимая во внимание, что
Ф(а) =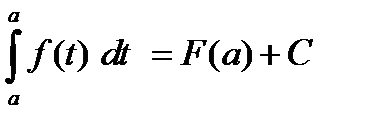 
= 0 (5.16)
из (5.16) получим:
- F (a) = C. (5.17)
Поскольку
Ф(b) = 
, (5.18)
то, подставив (5.17) в (5.18) получим формулу Ньютона – Лейбница
(5.19)
где F (x) - первообразная для функции f (x), а 
- знак подстановки Ньютона. Этот знак означает, что сперва в функцию F (x) подставляем верхний предел и вычитаем функцию вычисленную в точке нижнего предела.
Формула (5.19) дает следующее правило: для вычисления определенного интеграла необходимо найти первообразную подынтегральной функции, т.е. вычислить неопределенный интеграл, а затем вычислить разность значений первообразной на верхнем и нижнем пределе.
Пример 1. Вычислить интеграл 
.
Решение. 
. Следовательно, по формуле (5.19)
При вычислении определенного интеграла используются те же основные приемы, что и при вычислении неопределенного интеграла.
Формула интегрирования по частям в определенном интеграле
= 
- 
(5.20)
Пример 2. Вычислить 
Решение. Прямому вычислению данного интеграла препятствует наличие сомножителя х в подынтегральном выражении. Поскольку производная от х ’=1, то, используя (5.20), возьмем u = x. Тогда
=
Замена переменной в определенном интеграле. При вычислении определенного интеграла можно использовать замены, в том числе простейшие замены: линейную и «типа подведение под знак дифференциала».
= 
(5.21)
где x = j(t), j(a) = a, a=j-1(a); j(b) = b, b = j-1(b).
Пример 3. Вычислить 
.
Решение. Положив ln (х) = t, имеем 
. Если х = 1, то t = ln 1 = 0, если х = е, то t = ln е = 1. Тогда
Несобственные интегралы
Для существования определенного интеграла необходимо, чтобы промежуток интегрирования был конечен и подынтегральная функция ограничена. Когда не выполняется одно или оба эти условия, приходят к понятию несобственного интеграла.
Несобственные интегралы с бесконечными пределами. Пусть функция f (x) определена и непрерывна для всех х удовлетворяющих условию а £ х <+¥.
Рассмотрим интеграл 
. При изменении величины b этот интеграл будет вести себя как непрерывная функция от b. Если при бесконечном возрастании величины b существует конечный предел 
, то он называется несобственным интегралом от функции f (x) с бесконечным верхним пределом. Таким образом, по определению
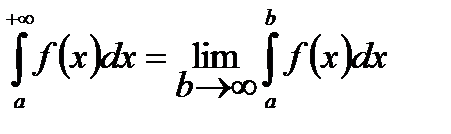. (5.22)
Если предел в (5.22) бесконечен или не существует, то говорят, что несобственный интеграл не существует или расходится.
Аналогичным образом определяются несобственные интегралы с бесконечным нижним пределом
,
и несобственный интеграл с двумя бесконечными пределами
.
Из определений несобственных интегралов непосредственно следует схема их вычисления: вначале находится первообразная F (x) для подынтегральной функции f (x), затем рассматривается разность пределов первообразных в точках верхнего и нижнего пределов интегрирования, т.е.
.
Пример. Установить, при каких значениях р сходится и при каких расходится интеграл 
.
Решение:
если p 
1, 
,
если p = 1, 
,
Вывод: сходимость интеграла I зависит от значения параметра р:
если р > 1, то 
, т.е. интеграл сходится,
если р < 1, то 
, т.е. интеграл расходится,
если р = 1, то 
интеграл расходится.
Несобственные интегралы от разрывных функций. Пусть функция f (x) определена и непрерывна на [ a,b ] за исключением точки с Î [ a,b ]. Рассмотрим три случая.
1. Функция терпит разрыв в точке b. Интеграл от функции f (x) с точкой разрыва на верхнем пределе определяется так
.
Пример. Вычислить интеграл 
.
Решение.
2. Функция терпит разрыв в точке а. Тогда по аналогии с предыдущим случаем интеграл с точкой разрыва на нижнем пределе определяется так
.
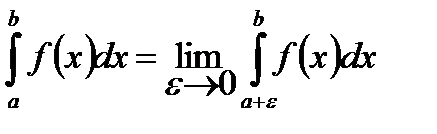Пример. Исследовать интеграл 
Здесь подынтегральная функция 
не существует в точке х = 0, поэтому
.
Таким образом, данный интеграл расходится (не существует).
Функция имеет разрыв во внутренней точке отрезка [ a,b ], т.е.
a < c < b.
.
Пример. Вычислить интеграл 
.
Решение. Подынтегральная функция терпит разрыв в точке 0. Поэтому
.
