Дифференциальное уравнение первого порядка - это уравнение, в которое входят независимая переменная, неизвестная функция и первая производная этой функции. Общий вид дифференциального уравнения первого порядка
F (x, y, y ¢) = 0.(6.7)
Здесь F - заданная функция трех аргументов. Она может не зависеть от x или y (или от обеих переменных), но должна содержать y ¢. Если уравнение (6.7) разрешить относительно y ¢, то получим разрешенный вид
y ¢ = f (x, y), (6.8)
где f - заданная функция от x и y или правая часть уравнения (6.8). В дальнейшем мы будем рассматривать только уравнения в разрешенном виде. Решение дифференциального уравнения (6.8) - это функция y = φ (x), которая, будучи подставлена в это уравнение, обращает его в тождество:
.
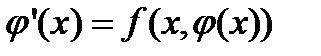Пример 1. Дано уравнение y ¢ + y ctg x - 2 cos x = 0.
Покажем, что функция y = sin x является его решением. Для этого подставим в данное уравнение вместо y и y ¢ функции sin x и (sin x)¢ = cos x. Получим
cos x + sin x ctg x - 2cos x = cos x + cos x - 2cos x º 0.
Уравнение обратилось в тождество.
Функция
y = j (x,C) (6.9)
называется общим решением уравнения (6.7), если она является решением этого уравнения при всех значениях произвольной постоянной C.
Если общее решение задано в неявном виде j (x, y, C) = 0, то оно называется общим интегралом. Частное решение уравнения (6.7) - это решение, которое получается из общего (6.9) при конкретном значении C.
Для дифференциального уравнения (6.7) задача Коши формулируется так: среди всех решений уравнения найти решение y = y (x), удовлетворяющее условию
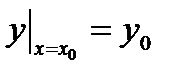(6.10)
где x 0, y 0 - заданные числа.
Условие (6.10) называется начальным условием, а числа x 0, y 0 - начальными значениями.
Уравнения с разделяющимися переменными - это уравнение, правая часть которого f (x, y) есть произведение двух сомножителей f (x) и g (y), каждый из которых зависит только от одной переменной
y ¢ = f (x) ∙ g (y).
(6.11)
Уравнения с разделяющимися переменными интегрируются следующим образом: y¢ заменяется на 
, затем умножаются обе части (6.11) на 
.
Получим:
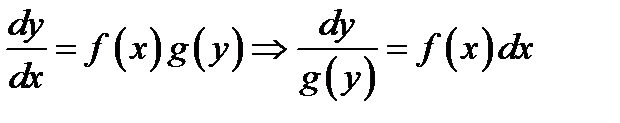(6.12)
Дифференциалы переменных x и y, и соответствующие функции стоят отдельно, т.е переменные отделены.
Если обозначить G (y) =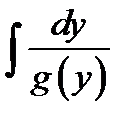 
, F (x) = 
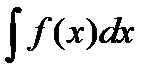, то уравнение (6.12) можно переписать в виде
dG (y) = dF (x).
Так как из равенства дифференциалов двух функций следует, что сами функции отличаются на произвольное постоянное слагаемое, то
G (y) = F (x) + C
или
. (6.13)
Выражение (6.13) представляет собой общий интеграл уравнения (6.11). Вычислив интегралы в (6.13), получим решение исходного уравнения
Пример 2. Решить уравнение 
.
Решение. Разрешим уравнение относительно y ¢: 
Здесь f (x) = -1/ х, а g(y) = y.
Заменим в этом уравнении y ¢ на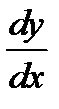 
и умножим обе части уравнения на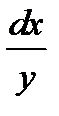 
.
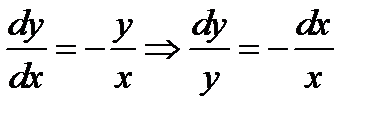Получили уравнение с разделенными переменными. Интегрируя, находим
,
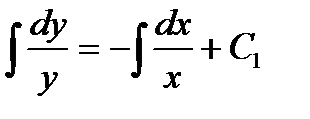где C 1 - произвольная постоянная.
Отсюда следует ответ: l n ½ y ½ = - l n ½ x ½ + C1. В данном случае удобно вместо C 1 написать C 1 = l n C 2 (C 2 > 0).
Тогда l n ½ y ½ = - l n ½ x ½ + l n C 2 или
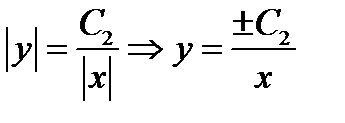
Так как ±C2 принимает любые значения, то обозначая ±C2 = C, окончательно получим
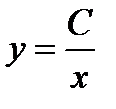
где C - произвольная постоянная.
Эта формула и дает общее решение заданного уравнения. Найдем теперь частное решение, удовлетворяющее начальному условию y ½ x =4 = 
. Для этого в равенство 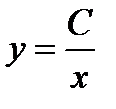подставим вместо x и y значения 4 и 
. Получим 
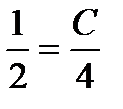. Отсюда следует, что C = 2. Таким образом, искомое частное решение имеет вид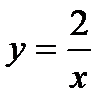 
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно искомой функции y(x) и ее производной y¢(x). В общем случае оно имеет вид
y ¢ + p (x) y = f (x).
(6.14)
Если f (x) º 0, то уравнение называется линейным уравнением без свободного члена (правой части) или линейным однородным уравнением. Итак,
y ¢ + p (x) y = 0
линейное однородное уравнение (оно же уравнение с разделяющимися переменными).
Если f (x) ¹ 0, то уравнение (6.14) называется линейным неоднородным уравнением.
Например, уравнение y ¢ - y cos2 x = х 2 является линейным неоднородным уравнением. Однородное по отношению к нему будет уравнение y ¢ - y cos2 x = 0. Уравнение (6.14) можно интегрировать разными методами. Мы рассмотрим метод Бернулли. Он состоит в следующем. В уравнении (6.14) делаем замену:
y = u (х) ∙ v (х). (6.15)
Дифференцируя по правилу «производная произведения двух функций», имеем
y ¢ = u ¢ (х) ∙v (х) + u (х) ∙ v ¢ (х)(6.16)
Подставим в уравнение (6.14) вместо y и y ¢ их выражения из (6.15) и (6.16), получим
u ¢ (х) v (х) + u (х) v ¢ (х) + p (х) u (х) v (х) = f (х)
или
u ¢ v + u [ v ¢ + p(x)v ] = f (х). (6.17)
Так как одну из функций в (6.17) можно выбрать произвольно, то функцию v выберем таким образом, чтобы коэффициент при u обратился в нуль, т.е.
v ¢ + p (x) v = 0. (6.18)
Уравнение (6.18) относительно функции v (x) является уравнением с разделяющимися переменными. Поэтому из (6.18) имеем:
Интегрируя, находим
Так как функция v - это любая функция, удовлетворяющая (6.18), то полагаем C = 0. Итак,
ln (v) = -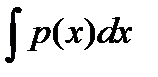 
Þ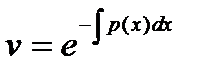 
.
Представляя найденную функцию v (x) в уравнение (6.17), получим
Отсюда следует
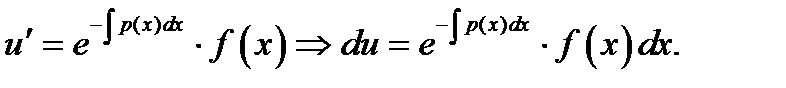
Интегрируя, получим
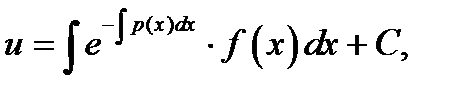(6.19)
где C - произвольная постоянная. Для того, чтобы найти y (x), умножим найденную u (x) на v (x):
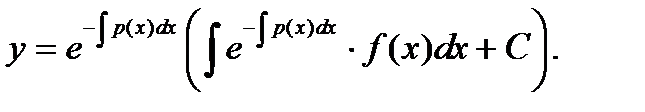(6.20)
Формула (6.20) дает общее решение дифференциального уравнения (6.14).
Пример. Найти общее решение уравнения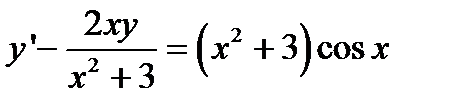 
.
Решение. Это линейное неоднородное уравнение, где
Выполнив замену y = u ∙ v, получаем y ¢ = u ¢ v + uv ¢.Заданное дифференциальное уравнение перепишем в виде
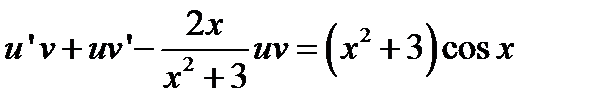
или
.
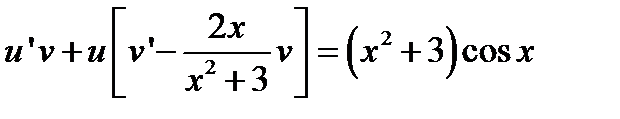Приравняем выражение в скобках нулю:
.
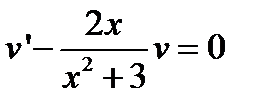Получили уравнение для функции v (x) - уравнение с разделяющимися переменными. Интегрируем его:
Подставляя функцию v (x) в уравнение, найдем уравнение для функции u (x):
u ¢(x 2 + 3) = (x 2 + 3) cosx.
Отсюда следует
u ¢ = cos(x) или u = 
Þ u = sin(x) + C.
Теперь находим общее решение заданного уравнения y (x):
y = uv Þ y = (sin (x) + C)∙(x 2 + 3).
