Дифференциальные уравнения второго порядка

 

Дифференциальное уравнение второго порядка - это уравнение, в которое входят независимая переменная, неизвестная функция, первая и вторая производные этой функции. Общий вид дифференциального уравнения первого порядка

 

                                                                       (6.21)

 

Здесь F - заданная функция четырех аргументов. Она может не зависеть от x, y и y’(или от обеих переменных), но должна содержать y’’.

Если уравнение (6.21) разрешить относительно , то получим разрешенный вид

 

y ’’ = f (x, y, y ’), (6.22)

 

где f - заданная функция от x, y и y ’. В дальнейшем мы будем рассматривать только уравнения в разрешенном виде.

Решение дифференциального уравнения (6.22) - это функция , которая, будучи подставлена в это уравнение, обращает его в тождество:

 

                                                                      (6.23)

 

Определение. Общим решением уравнения второго порядка называется такая функция

 

,                                                                           (6.24)

 

которая при любых значениях произвольных постоянных C ₁и C ₂ является решением этого уравнения.

Если заданы начальные условия (это называется задача Коши) , то подставляя начальные условия в общее решение, получим частное решение. Конкретные значения постоянных C ₁и C ₂ находятся из системы

 

 

Определение. Линейным неоднородным уравнением второго порядка называется уравнение

 

,                                                    (6.25)

 

где p (x), q (x) – коэффициенты уравнения, а f (x) – правая часть уравнения.

Если f (x) =0, то уравнение называется однородным

 

                                                              (6.26)

 

Если коэффициенты p (x) и q (x) постоянны, т.е. не зависят от х, то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:

 

.                                                                                (6.27)

Решением такого уравнения может быть только функция не меняющая свой вид при дифференцировании, т. е.

 

.                                                      (6.28)

 

Подставляя функцию и производные в уравнение (6.28), получим

 

.

 

В этом выражении при любых значениях k и x, поэтому на него можно сократить.

Уравнение

 

                                                                             (6.29)

 

которое получается из линейного однородного уравнения, называется характеристическим уравнением.

Известно, что квадратное уравнение имеет решение, зависящее от дискриминанта :

Если , то корни k ₁ и k ₂ - действительные различные числа.

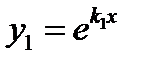. Следовательно решениями будут функции и .

В качестве общего рещения берется их линейная комбинация с произвольными постоянными C ₁и C ₂

 

.                                                                    (6.30)

Если , то k₁ = k₂, . Тогда в качестве общего решения берется следующее выражение

 

                                                                         (6.31)

 

Если , то решениями уравнения будут два комплексных числа

, где введены обозначения , , а  .

В этом случае можно использовать формулу (6.30), подставляя , а , но удобнее сделать преобразование и записать общее решение в виде

 

                                               (6.32)

Пример 1. Найти общее решение уравнения .

Решение. Ищем решение уравнения в виде  тогда  и, подставляя в исходное уравнение получим  Так как  то на него можно сократить и мы получим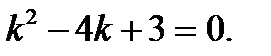

Находим его корни

Корни характеристического уравнения вещественные, различные, значит, общее решение дифференциального уравнения имеет вид

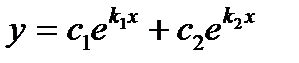
или

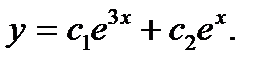
Пример 2. Найти общее решение уравнения

Решение. Составляем характеристическое уравнение (см. пример 1)

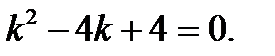
Решаем его

Корни характеристического уравнения вещественные равные. Общее решение дифференциального уравнения имеет вид

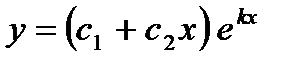
или

Пример 3. Найти общее решение уравнения

Решение. Составляем характеристическое уравнение (см. пример 1)

Корни характеристического уравнения комплексные сопряженные, значит, общее решение дифференциального уравнения имеет вид

Пример 4. Найти частные решения однородных линейных дифференциальных уравнений второго порядка, удовлетворяющие указанным начальным условиям:

 где

 где

Решение. а) находим общее решение (см. пример 1)

Общее решение

Дальше решаем задачу Коши. Постоянные  найдем с помощью начальных условий, вычислив предварительно производную от общего решения

Подставляя начальные условия в общее решение и его производную, получим

.

Из этой системы находим

Подставив значения постоянных в общее решение, получим искомое частное решение

b) решаем второе уравнение. Его характеристическое уравнение имеет вид

Находим корни:  Общее решение

Вычисляем:

Подставляя начальные условия, получаем

Частное решение

 

Общим решением неодногодного уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного уравнения.

Укажем способ, позволяющий найти частное решение неоднородного уравнения по виду правой части. Заметим, что это возможно лишь в случаях, когда правая часть уравнения является функцией определенного вида.

Пусть

Тогда частное решение ищут в виде 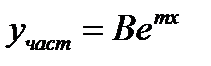. Коэффициент В находят непосредственной подстановкой частного решения в уравнение. Общее решение имеет вид

, .

Тогда частное решение ищут в виде

.

Если , то

.

Если справа стоит сумма или произведение двух функциий, то в качестве частного решения берется соответственно сумма или произведение соответствующих функций.

Пример 5. Найти общее решение уравнения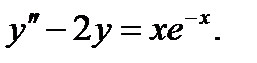

Решение. Находим сначала общее решение соответствующего однородного уравнения

Характеристическое уравнение  Его корни

Общее решение однородного уравнения

Теперь следует найти частное решение  неоднородного уравнения. Правая часть  значит  ищем в форме , т.к.  не является корнем характеристического уравнения.

Требуется найти неизвестные коэффициенты А и В. Для определения А и В дифференцируем дважды

и подставляем это в данное неоднородное уравнение:

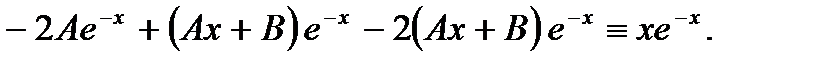
Так как  то сократив , получим тождественное равенство двух полиномов

Значения А и В найдем, приравнивая коэффициенты при одинаковых степенях  в левой и правой частях

при Х:

при Х ⁰: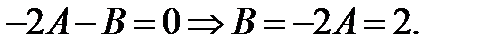

Подставляем найденные А и В в

Общее решение неоднородного уравнения

Пример 6. Найти общее решение уравнения

Решение. Соответствующее однородное уравнение

Составляем характеристическое уравнение и решаем его

Правая часть данного неоднородного уравнения

Следовательно, частное решение  разыскиваем в виде

,

т.к. 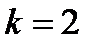 не является решением характеристического уравнения.

Дифференцируем и подставляем это решение в неоднородное уравнение

Приравниваем коэффициенты при одинаковых тригонометрических функциях в левой и правой частях тождества

при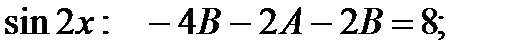

при

Из этой системы находим А и В

Общее решение

Пример 7. Найти частное решение уравнения  удовлетворяющее начальным условиям

Решение. Чтобы найти частное решение, удовлетворяющее заданным начальным условиям, необходимо получить сначала общее решение данного неоднородного уравнения. Находим его (см. пример 6)

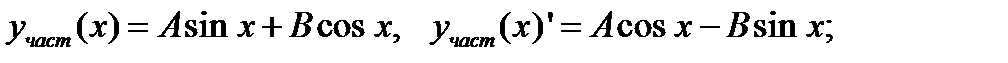
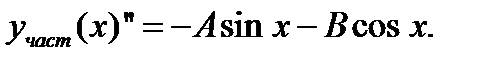
Подставляем  в уравнение

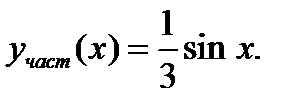
Искомое частное решение будем находить из общего. Общее решение неоднородного уравнения

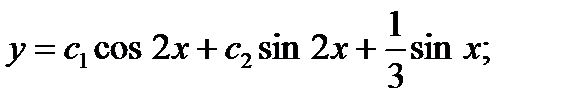
Подставляем начальные условия. При  имеем

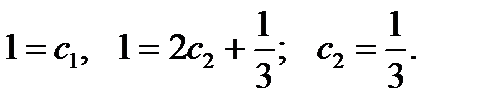
Найденные постоянные подставляем в общее решение неоднородного уравнения

искомое частное решение.