Для дифференцируемых функций выполняется ряд важных для приложений теорем. Перечислим основные теоремы.
Теорема Вейерштрасса.
Если функция непрерывна на замкнутом промежутке [ a, b ], то она достигает на этом промежутке наибольшего M и наименьшего m значений.
При этом могут возникать три случая.
1. Наименьшее и наибольшее значения достигаются внутри промежутка [ a, b ] (рис.2.3 а).
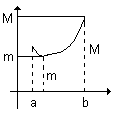
а б в
Рис. 2.3. Наибольшее и наименьшее значение функции на интервале.
2. На границе достигается либо только наибольшее, либо только наименьшее значение (рис. 2.3 б).
3. На границе достигается и наибольшее и наименьшее значение (рис. 7.3в).
Теорема Роля
Пусть функция у = f (x):
1. непрерывна на отрезке [ a, b ],
дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a, b),
2. f (а) = f (b).
Тогда внутри отрезка (a, b) существует по крайней мере одна точка с,
a < c < b в которой производная обращается в ноль f `(c) = 0.
Замечание. Точка с является корнем производной. Если f(а) = f(b) =0, то теорема формулируется так: между корнями функции лежит корень производной.
Доказательство. Функция у = f (x) непрерывна на промежутке [ a, b ], то, по теореме Вейерштрасса, она достигает на нем своего наибольшего и наименьшего значений. Но так как значения функции на концах промежутка совпадают, то исключен третий случай теоремы Вейерштрасса, т.е. одно из значений – наибольшее или наименьшее – достигаются внутри промежутка. Предположим, что внутри в точке с, a < c < b достигается наибольшее значение М = f (с), остальные случаи доказываются аналогично. Докажем, что в точке с производная обращается в ноль.
Возьмем два значения аргумента х 1 > c, х 2< c (рис. 2.4).
Для х 1:D x = х 1 – с, D x > 0, D f (x) = f (х 1) - f (с) = f (х 1) - М < 0.
Следовательно 
Для х 2:D x = х 2 – с, D x < 0, D f (x) = f (х 2) - f (с) = f (х 2) - М < 0.
Следовательно 
Тем самым, в точке с производная равна нулю f `(c) = 0.
Рис. 2.3. Теорема Ролля.
Замечание. В точке с касательная идет горизонтально параллельно оси ОХ.
Формула Лагранжа (формула конечных приращений). Пусть функция у = f (x) непрерывна на отрезке [ a, b ], дифференцируема во всех внутренних точках отрезка, т. е. в интервале (a, b), то внутри отрезка существует по крайней мере одна точка с, a < c < b в которой справедливо равенство: полное приращение функции равно производной, вычислленной в точке с, умноженной на длину промежутка
f (b) - f (а) = f `(c)(b - а). (2.18)
В точке с касательная параллельна секущей MN (см. рис. 2.4).
Рис. 2.4. Геометрический смысл формулы конечных приращений.
Теорема Коши. Пусть функции f (x) и g (x) непрерывны на отрезке [ a,b ], причем g (x) ≠ 0, дифференцируемы во всех внутренних точках отрезка, т. е. в интервале (a, b), то внутри отрезка существует точка с, a < c < b в которой справедливо равенство
(2.19)
Правило Лопиталя. Пусть функции f (x) и g (x) на отрезке [ a, b ] удовлетворяют условию теоремы Коши и f (с) = g (с) = 0 (a < c < b), то если существует предел отношения производных при х →с, то существует и придел отношения функций в этой точке, причем
(2.20)
Замечание. Правило Лопиталя можно применять и для раскрытия неопределенностей типа 
.
Пример. Вычислить предел 
.
Решение. Так как е-х = 1/ех, то предел можно преобразовать к виду
.
Формула Тейлора. Пусть функция у = f (x) в интервале (a,b) имеет производные до (n +1) ˗ го порядка включительно. Приближающий полином n ˗ ой степени, значение которого и его производных до порядка n включительно совпадают со значением функции и ее производных в точке x 0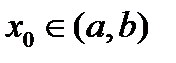 
имеет вид
(2.21)
… 
В окрестности точки х0 замена функции полиномом (2.21) дает некоторую ошибку. Формула Тейлора обеспечивает возможность точной замены данной функции полиномом
… 
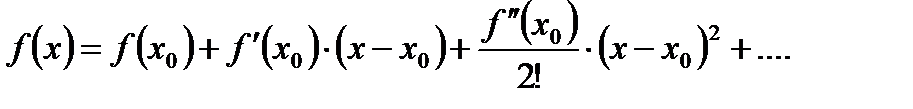
(2.22)
где a < x < b, a<x 0 <b, x 0 <c<x.
Выражение
(2.23)
называется остаточным членом формулы Тейлора в форме Лагранжа. Величина Rn (x).определяет погрешность, возникающую при замене функции полиномом степени n из (2.23). Форма Лагранжа позволяет при вычислениях найти оценку сверху для ½ Rn (x)½.
Если учесть, что
Δ х = х – х 0,
Δ f (x) = f (x) - f (x 0),
d n f (x)= f n(x)Δ х,
то получим дифференциальную форму формулы Тейлора
(2.24)
Формула Маклорена - частный случай формулы Тейлора, когда x 0 = 0.
(2.25)
Пример. Вычислить значение числа е.
Решение. Построим формулу Тейлора для функции f (x) = ex в окрестности точки х0 = 0. Прежде всего, вычислим производные:
f (x) = ex, f ¢(x) = ex, f ¢¢(x) = ex,..., f (k)(x) = ex.
Отсюда
f (0) = f ¢(0) = f ¢¢(0) =... = f (k)(0) = 1.
Из (2.25) для f (x) = ex имеем
Эта формула получена для ex. Если в правой части положить х = 1, то
В зависимости от требований задачи эта формула позволяет получить сколь угодно точные значения величины e. Так
для n = 2 е» 2.5, ошибка не превышает величины 0.23,
для n = 3 е» 2.667, ошибка не превышает величины 0.052,
для n = 10 е» 2.7182818 и ошибка не более, чем 4.3 ּ 10-7.
