Основные понятия теории дифференциальных уравнений.
Пусть x - независимая переменная, y(x) - неизвестная функция этой переменной. y¢, y¢¢,..., y(n) - производные неизвестной функции. Уравнение, связывающее независимую переменную х с функцией y (x) и ее производными до порядка n включительно, называется обыкновенным дифференциальным уравнением.
F (x, y, y ¢, y ¢¢,..., y ( n )) = 0. (6.1)
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.
Дифференциальное уравнение n -го порядка может не содержать некоторые из величин x, y, y ¢,..., y (n -1) или даже все эти величины, но оно обязательно содержит n -ю производную y (n).
Пример 1. y ¢ + 2 y = 0 - уравнение 1-го порядка, так как наивысший порядок производной равен единице.
Пример 2. y (4) - y ¢ = 0 - уравнение 4-го порядка: входят производные 1-го и 4-го порядков, наивысший порядок производной равен 4.
Решение дифференциального уравнения - это функция 
, которая, будучи подставлена в уравнение, обращает его в тождество:
Пример 3. Пусть дано уравнение y ¢¢ + y = 0. Проверим непосредственной подстановкой, что функция y = sinx является решением этого уравнения.
y ¢= (sin x)¢ = cosx, y ¢¢= (cosx)¢= - sinx.
Подставим в уравнение вместо y и y ¢ функции sinx и - sinx:
- sinx + sinx º 0.
График решения называется интегральной кривой. Задача нахождения решений дифференциального уравнения называется задачей интегрирования дифференциального уравнения.
Рассмотрим уравнение n -го порядка, разрешенное относительно старшей производной:
y ( n ) = f (x, y, y ¢,..., y ( n -1)).
(6.2)
Такая запись уравнения называется видом, разрешенным относительно старшей производной, а функция f (x, y, y ¢,..., y ( n -1)) называется правой частью уравнения.
Предполагаем, что функция f определена, однозначна и непрерывна в некоторой области изменения своих аргументов. Задача нахождения решения y = y (x), удовлетворяющего заданным начальным условиям: при x = x 0
y = y 0,
y ¢= y 1¢,
...,
y ( n -1) = yn (6.3)
где x0, y 0, y 1,..., yn - заданные числа (начальные данные), называется задачей Коши.
Начальные условия можно записать и так:
Дадим определения общего и частного решений уравнения n -го порядка
правая часть которого 
есть функция определенная и непрерывная в некоторой области G изменения переменных x, y, y ¢,..., y (n -1). Функция
y = j (x,C1,C2,...,C n),(6.4)
зависящая от аргумента x и n произвольных постоянных C 1, C 2,..., Cn, называется общим решением уравнения (5.2) в области G, если она удовлетворяет двум условиям:
1) функция (6.4) является решением уравнения (6.2) при любых значениях произвольных постоянных C 1, C 2,..., Cn;
2) каковы бы ни были начальные условия (6.3), существует единственный набор постоянных C 10, C 20,..., Cn 0, такой, что функция y = j (x,C10, C20,..., Cn0) является решением уравнения (6.2) и удовлетворяет начальным условиям (6.3).
Чтобы найти решение уравнения (6.2) с начальными данными (x 0, y 0, y 1, yn ) из области G, если известно общее решение (6.2) поступают следующим образом:
составляют систему уравнений
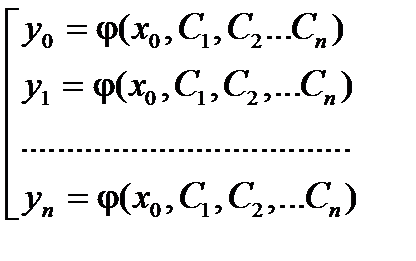(6.5)
2) решая систему (6.5), находят C 10, C 20,..., Cn 0;
3) подставляют найденные значения произвольных постоянных в общее решение(6.4) и получают искомое решение
y = j (x,C10, C20,..., Cn0),
которое является искомым единственным решением задачи.
Если общее решение уравнения (6.2) задано в неявном виде
Ф (x, y,C1, C2,..., C n) = 0,(6.6)
то оно называется общим интегралом дифференциального уравнения.
Всякое решение, получаемое из общего решения (6.4) при конкретных значениях постоянных C 1 = C 10, C 2 = C 20,..., Cn = Cn 0, называется частным решением уравнения (6.2).
