Основные методы интегрирования

 

Для вычисления неопределенных интегралов часто используют так называемые стандартные методы интегрирования. Перечислим основные из них.

Метод замены переменной. Добиться упрощения подынтегрального выражения можно при помощи замены переменной интегрирования. Суть этого метода заключается в замене переменной интегрирования х на некоторую непрерывную функцию х = j(t), имеющую непрерывную производную φ’(t) и обратную функцию 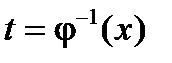, с тем, чтобы преобразовать исходный интеграл к более простому виду. Тогда  и

 

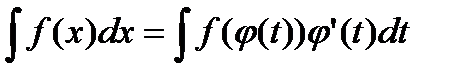                                                                      (4.10)

 

Формула (4.10) называется формулой замены переменной под знаком неопределенного интеграла. Для доказательства, как мы это делали ранее, возьмем производные по переменной х от левой и правой части и проверим, что они совпадают (формулы 4.5, 4.6)

 

Для вычисления производной от правой части вспомним, что . Тогда

 

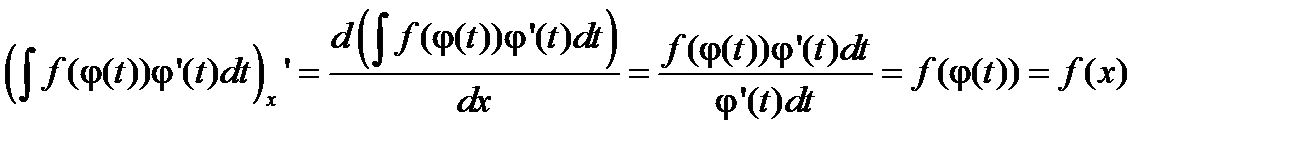
Алгоритм метода замены переменной следующий. Вначале необходимо найти замену переменной интегрирования x = j(t), записать интеграл с новой переменной интегрирования t, вычислить его, а затем вновь вернуться к исходной переменной интегрирования, использовав обратную функцию .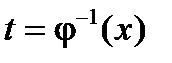

Простейшие замены. К простейшим относятся линейная замена и замена типа «подведение под знак дифференциала».

Линейная замена основана на следующем соотношении. Пусть интеграл

 

 

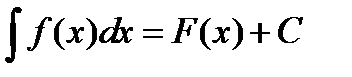
является табличным. Тогда можно вычислить интеграл от функции f (ax + b)

 

.                                                             (4.11)

 

Для доказательства возьмем производные от левой и правой части равенства (4.11)

 

.

.

Пример 1. Вычислить .

Решение. За базовый возьмем табличный интеграл

.

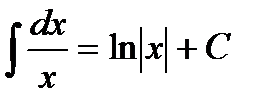Тогда

.

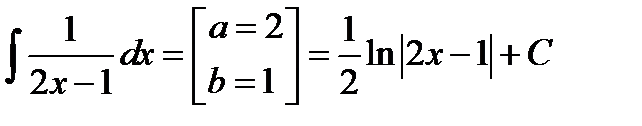Пример 2. Вычислить .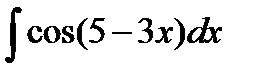

Решение. За базовый возьмем табличный интеграл

.

Тогда

 

.

 

Замена типа подведение под знак дифференциала основана на формуле

          (4.12)

 

т.е. в данном случае сделав замену 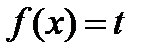, x = f ^{– 1}(t) мы проверяем, есть ли под знаком интеграла dt, а не находим dx.

Пример 3. Найти .

Решение. Особенностью данного интеграла является то обстоятельство, что его подынтегральное выражение содержит сомножитель 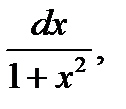 который является дифференциалом функции arctg x. Поэтому в данном интеграле целесообразно ввести замену переменной:

 

t = arctg x.

 

Отсюда

dt = d (arctg(x)) = и e ^{arctg x} = e^t.  

Подставляя в исходный интеграл, имеем 

 

 = e ^{arctg x} + C.

 

Пример 4. Найти .

Решение. Здесь уместна замена

 

t = cos x,

 

т.к. dt = - sin x d x, и sin³ x d x = sin² x sin x d x = (1 – cos²(x)) sin xdx.

 

Поэтому

 

 

Метод интегрирования по частям. Пусть u (x) и v (x) две дифференцируемые функции. Метод интегрирования по частям позволяет вычислять интегралы от произведений функций и основан на формуле

 

                                                               

или, в развернутом виде,

 

                                  (4.13)

 

Эта формула носит название формулы интегрирования по частям. Ее применение полезно в тех случаях, когда подынтегральное выражение можно представить в виде произведения двух функций и выражение  для взятия интеграла проще, чем подынтегральное выражение .

Доказательство. По правилу дифференцирования произведения функций u (x) и v (x), имеем

 

.

 

Проинтегрируем это равенство, учитывая, что (4.7)

 

.

 

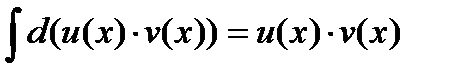Тогда

 

.

 

Из этого соотношения легко получить формулу (4.13).    

 

Пример 5. Найти .

Решение. Использование формулы интегрирования по частям позволяет вместо исходного не табличного интеграла вычислить только интеграл от sin x. Покажем это, приведя схему записи удобную при использовании метода интегрирования по частям.

 

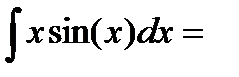
= - x ∙cos(x) +  =

 

= - x ∙ cos(x) + sin(x)+ C.

 

Обычно в интегралах за u (x) берут следующие функции:

ln(x), arсsin(x), arсcos(x), arсtg(x), arсctg(x)

а за v’(x) берут функции е ^х, sin(x), cos(x).

Функцию х ⁿ, где n натуральное число, можно относить и к первой и ко второй группе.

Метод разложения на простейшие. Правильной рациональной дробью R (x) называется отношение двух полиномов (многочленов)

 

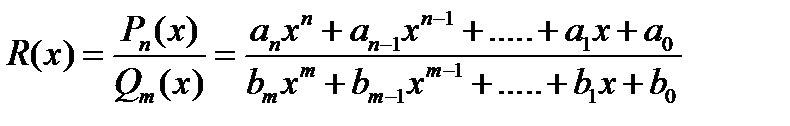                                (4.14)

 

где  коэффициенты многочленов  и .

Если 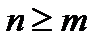дробь называется неправильной, такие дроби необходимо упростить, выделив целую часть и остаток в виде правильной дроби.

Знаменатель рациональной дроби имеет ровно n корней, среди которых есть действительные корни (кратные, т.е. повторяющиеся, и некратные) и комплексные корни, также кратные и некратные (комплексные корни являются корнями квадратного трехчлена с отрицательным дискриминантом).

Простейшими дробями или просто простейшими называются дроби вида

1. ,

соответствует действительному некратному корню знаменателя а,

2. , k – целое положительное число,

соответствует действительному кратному корню знаменателя а, число k называется кратностью корня,

3. , где знаменатель  имеет только комплексней корни, т.е. ,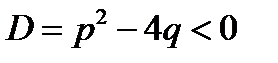

соответствует двум комплексным некратным корням,

4. , k – целое положительное число,

соответствует двум комплексным кратным корням, число k кратность корня.

Всякую правильную рациональную дробь можно представить в виде суммы элементарных дробей, поэтому приведем интегралы от первых трех видов простейших

1. .                                                     (4.15)

2. .             (4.16)

3. .          (4.17)

 

Пример 6. Вычислить .

Решение. Используем формулу (4.15)

.

Пример 7. Вычислить .

Решение. Используем формулу (4.16)

.

Пример 8. Вычислить .

Решение. Так как , то используем формулу (4.17)

 

Приведем примеры разложения правильной рациональной дроби на простейшие слагаемые, исходя из следующего правила:

каждому некратному корню соответствует простейшая первого вида,

каждому кратному корню кратности k соответствует k -1 простейшая второго вида с убывающими степенями знаменателя и одна простейшая первого вида,

каждым двум некратным комплексным корням соответствует простейшая третьего вида.

Пример 9. Разложить на простейшие рациональную дробь .

Решение. Корни знаменателя: х ₁ = -1 действительный некратный корень, и х ₂ = 0 действительный кратный корень кратности 2. Следовательно

 

.

Для того, чтобы найти неизвестные коэффициенты А, В ₁ и В ₂ приведем правую часть выражения к общему знаменателю, раскроем скобки и приведем подобные члены в числителе

 

.

Приравняем числители исходного и конечного выражений

 

.

 

Такое соотношение возможно тогда и только тогда когда совпадают коэффициенты при одинаковых степенях х (если какая-то степень х отсутствует, то это значит, что коэффициент при ней равен нулю). Получим систему

 

.

 

Окончательно

 

.

Пример 10. Разложить на простейшие рациональную дробь .

Решение. Корни знаменателя: х ₁=0 действительный некратный корень, и два комплексных корня квадратного трехчлена 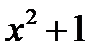 с отрицательным дискриминантом

 

.

 

Для того, чтобы найти неизвестные коэффициенты А, В и D приведем правую часть выражения к общему знаменателю, раскроем скобки и приведем подобные члены

 

.

 

Приравняем числители и коэффициенты при одинаковых степенях х

 

.

 

Получим систему

Окончательно

 

.

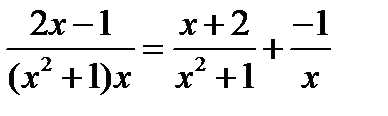Вычислим интегралы от рациональных дробей примеров 9 и 10, используя формулы (4.15-4.17)

,

.

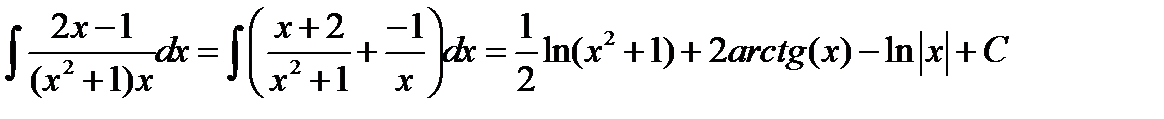Замечание. Существует большое количество интегралов, которые методом замены переменной можно свести к интегралам от рациональных дробей. К таким интегралам относятся интегралы от иррациональных функций вида

В этом случае надо сделать замену переменной вида , где r – общий знаменатель дробей m / n, k / s …

Пример. Вычислить интеграл .

Решение. Степени корней ¼ и 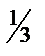 имеют общий знаменатель 12. Следовательно, замена

=

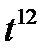
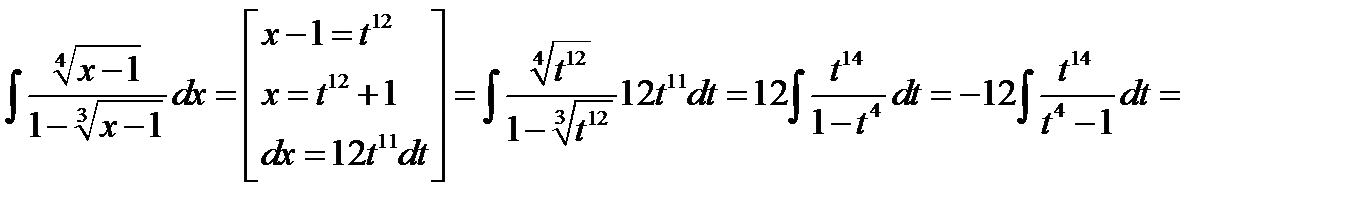
Получили неправильную рациональную дробь. Разделим числитель на знаменатель

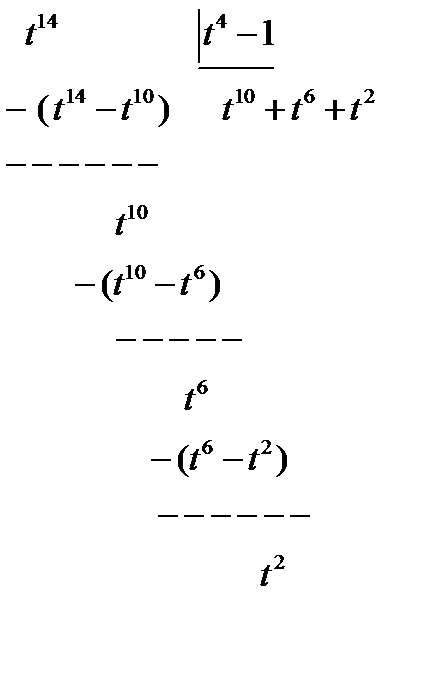
Следовательно  

 

.

 

Продолжим вычисление интеграла

 

Вычислим отдельно интеграл от правильной рациональной дроби методом разложения на простейшие. Знаменатель имеет корни: t ₁= 1, t ₂= -1 и два комплексных корня, соответствующих множителю t ²+ 1.

 

.

 

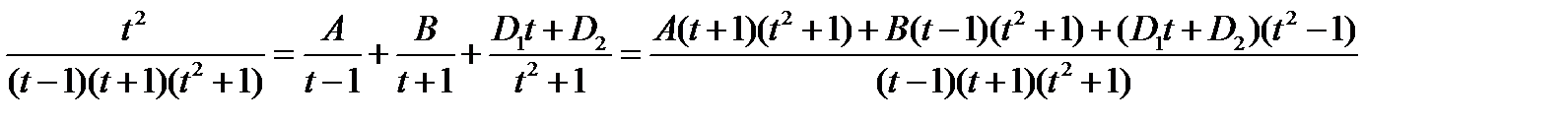Раскрыв скобки и приведя подобные члены получим

Подставим полученное разложение рациональной дроби в интеграл

 

 

 

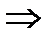
Определенный интеграл.