1. Вычисление площади плоских фигур. Как уже отмечалось, если f (x) ³ 0 на отрезке [ a,b ], то определенный интеграл от функции численно равен площади криволинейной трапеции, ограниченной кривой y = f (x), осью абсцисс и прямыми x = a, и x = b.
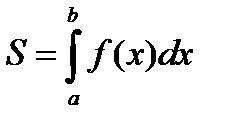(5.23)
Если на [ a,b ] функция, как показано на рис. 5.6, меняет знак, то необходимо вычислить интеграл от модуля подинтегральной функции.
.
Это означает, что если на отрезке [ а,с ] Ì [ a, b ] функция f (x) < 0, то на этом отрезке берется отрицательное значение функции
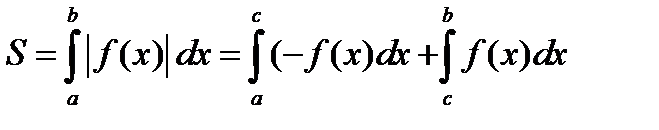
Пример 1. Вычислить площадь, ограниченную осью абсцисс и синусоидой на отрезке [0,2p].
Решение. Поскольку sin(x) ³ 0 на отрезке [0, p] и sin(x) £ 0 на [p,2p], то искомая площадь S равна
S =
= - (cosp - cos0) + (cos2p -cosp) = -(-1 –1) +(1 + 1) = 4.
Рис. 5.6. Вычисление площади при помощи определенного интеграла
Рис. 5.7. Вычисление площади плоской фигуры.
В более общем, случае требуется вычислить площадь плоской фигуры ограниченной несколькими кривыми линиями. В этом случае искомая площадь есть алгебраическая сумма площадей нескольких криволинейных трапеций. Например, как показано на рис.5.7
Пример 2. Вычислить площадь фигуры, ограниченной функциями y 1=½ x - 2½ и y 2 = 
(рис. 5.8).
Рис. 5.8. Площадь плоской фигуры.
Решение. Найдем точки пересечения линий. Для этого решим уравнение
y 1(х) = y 2(х).
Возведем в квадрат левую и правую часть
или 
; 
.
Учтем, что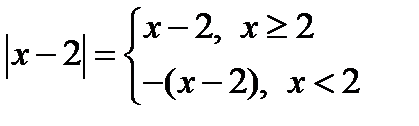 
.
Следовательно
Вычисление длины дуги. Пусть некоторая гладкая плоская кривая описывается функцией f (x) и отрезку [ a,b ] оси абсцисс отвечает дуга AB. Произвольным образом разобьем эту дугу, как показано на рис.5.9 на n частей точками M 0, M 1,..., M n. Получим элементарные дуги. Соединив каждые две соседние точки прямой, получим вписанную в дугу AB ломаную линию. Длину звена ломанной D l i, лежащую между точками М i Mi + 1, где М i (xi, f (xi)), М i +1 (xi + 1, f (xi +1)) находим по формуле
.
Длина элементарной дуги М i Mi +1 примерно равна D l i
. (5.24)
Просуммируем (5.24) по всем элементарным дугам, тогда длина L дуги АВ равна
Рис. 5.9. Длина дуги.
.
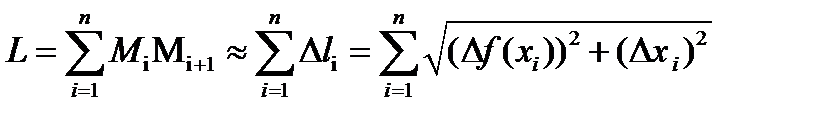Выражение, стоящее в правой части равенства является интегральной суммой. При бесконечном увеличении числа точек разбиения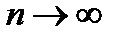 
, проводимого произвольным образом, если каждый раз длина самой большой элементарной дуги r будет стремится к нулю 
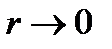,то длина ломаной будет неограниченно приближаться к длине дуги. Тогда длина дуги L плоской кривой
(5.25)
Если кривая задана в параметрическом виде: х = j(t), y = y(t) (a£ t £b), то длина кривой вычисляется по формуле
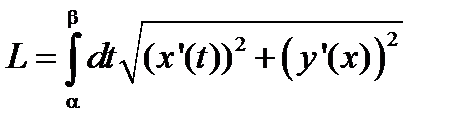(5.26)
Пример 1. Найти длину дуги кривой y 2 = x 3 , заданной на отрезке от x = 0 до x = 1 (y ³ 0).
Решение.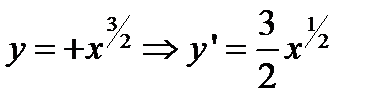 
. Подставляя затем этот результат в (5.25), получим
.
Пример 2. Найти длину дуги кривой x = a cos3 t, y = a sin3 t, если t изменяется 0 до p/2.
Решение. Вначале находим производные по t
x ¢(t) = -3 a cos2 t ּsin t, y ¢(t) = 3 a sin2 t ּcos t
Подставляя в формулу (5.26), имеем
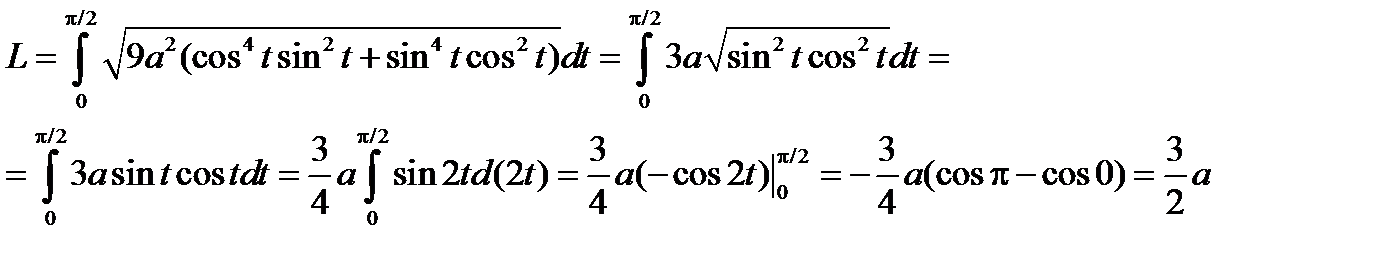
Вычисление объемов тел. Пусть дано тело переменного сечения, расположенной над осью ОХ (рис.5.10), ограниченное плоскостями х = а и х = b. Объем тела обозначим за V. Разделим отрезок [ a, b ] на произвольные n частей, при этом координаты точек деления удовлетворяют соотношению
x 0 = a < x 1 < x 2 <... < x i -1< x i <... < x n = b.
Рис. 5.10. Объем тела переменного сечения.
В точках деления проведем плоскости, перпендикулярные оси О Х. Тело разделится на n узких слоев (элементарных объемов) шириной Δ x i = x i - x i-1 (i = 1, 2,…, n). Объем каждого такого слоя обозначим как Δ V i. На каждом промежутке [ x i-1, x i] выберем произвольную точку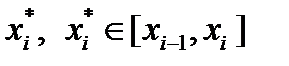 
. Обозначим за S (x *i) площадь поперечного сечения тела в этой точке. Тогда
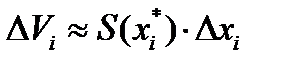(5.27)
Просуммируем (5.27) по всем i, получим интегральную сумму
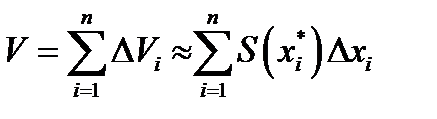(5.28)
Увеличим число разбиений n. При этом каждый раз обязательно должна уменьшатся длина наибольшего из разбиений Δ x i, т.е. ранг дробления r должен стремится к нулю. Тогда объем тела переменного сечения V,будет равен пределу интегральной суммы при 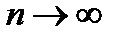и
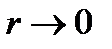
(5.29)
Если тело получено при вращении криволинейной трапеции вокруг оси ОХ (рис. 5.11), то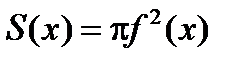 
. В этом случае объем тела V вычисляется по формуле
(5.30)
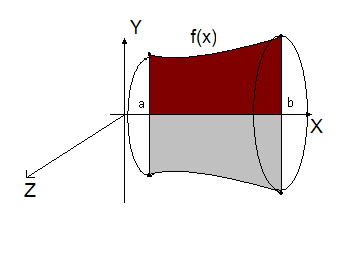
Рис. 5.11. Объем тела вращения.
Пример. Вычислить объем тела, полученного при вращении кривой y = sin(x) вокруг оси ОХ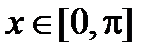 
.
Решение.
.
