Определение первообразной. Определение определенного интеграла. Вычисление неопределенного интеграла

 

Функция F (x), производная которой равна функции f (x), т.е.

 

F ¢(x) = f (x)                                                                                  (4.1)

 

называется первообразной для f (x). Так, например, если , то ее первообразная есть 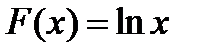, так как

, .

 

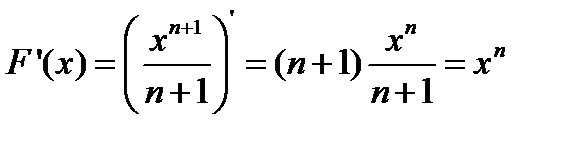Если же f (x) = sin (2 x), то ее первообразная F (x) = - 0.5 cos(2 x), так как

 

.

 

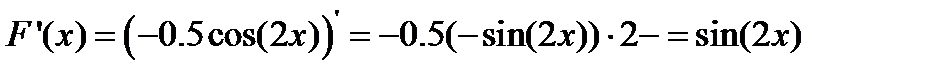Теорема. Пусть F ₁(x) и F ₂(x) две разные первообразные одной и той же функции f (x) на промежутке [ a, b ]. Тогда разность между ними есть постоянная величина С.

Доказательство. Обозначим за Ф(х) разность между F ₂(x) и F ₁(x), т.е. Ф(х) = F ₂(x) - F ₁(x) и возьмем производную от функции Ф(х)

 

                                 (4.2)

Единственной функцией, производная которой при любом значении х равна нулю, есть постоянная величина, следовательно Ф(х) = const ≡ C и 

F ₂(x) = F ₁(x) + С.                                                                       (4.3)

 

Следствие. Функция f (x) имеет бесконечное множество первообразных { F (x)}, отличающихся на постоянную величину, т.е. { F (x)}= F (x) + C.

Пример. Для f (x) = sin(2x) первообразной будет не только функция F (x) = – 0.5 cos(2 x), но и функция F (x) = – 0.5 cos(2 x) +4, F (x) = – 0.5 cos(2 x) -1, и. вообще, любая функция вида F (x) = – 0.5 cos(2 x) + C

 

Множество всех первообразных { F (x)} функции f (x) называется неопределенным интегралом от этой функции и обозначается так

 

,                                                                                (4.4)

 

где ò - знак интеграла, читается “интеграл”,

f (x) - подынтегральная функция от переменной интегрирования х,

f (x)d x - подынтегральное выражение,

C - постоянная интегрирования.

Из определения интеграла следует, что

Производная от неопределенного интеграла равна подинтегральной функции. Действительно

 

()¢ = (F (x) + C)¢ = F ¢(x) + 0 = f (x).                                       (4.5)

 

Дифференциал от неопределенного интеграла равен подинтегральному выражению. Действительно, так как d F = F ¢(x)d x, получим

 

d () = ()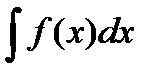¢ d x = f (x) dx.                                      (4.6)

 

Интеграл от дифференциала первообразной равен самой первообразной. Действительно, пусть F (x) - первообразная для функции f (x) (т.е. F ¢(x) = f (x)). Тогда

 

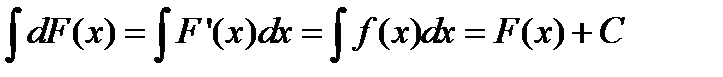                                  (4.7)

                                                       

Формулы (4.5 – 4.7) наглядно иллюстрируют то обстоятельство, что операции дифференцирования и интегрирования взаимно обратны с точностью до постоянной. В этой связи по аналогии с таблицей формул дифференцирования элементарных функций можно построить таблицу основных интегралов.

Линейные свойства неопределенного интеграла.

Интеграл о суммы функций равен сумме интегралов.

 

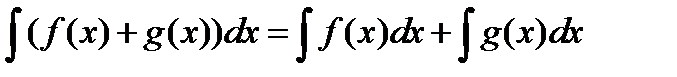                                            (4.8)

 

Постоянный множитель можно выносить за знак неопределенного интеграла.

 

                                                                 (4.9)

                                                                     

Справедливость равенств (4.8) и (4.9) проверяется дифференцированием. Возьмем производную от левой и правой части равенства (4.8) и проверим, что они совпадают. По правилу (4.5)

 

 

 

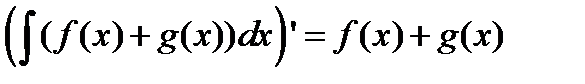
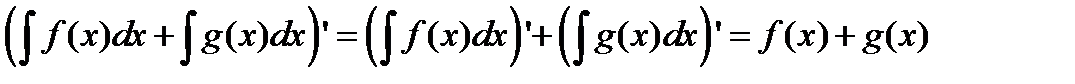
Если совпадаю производные, то и первообразные равны с точностью до постоянной. Равенство (4.9) доказывается аналогично. Основные простейшие интегралы сведены в табл. 3.

Пример. Найти .

Решение. Запишем стоящую в числителе единицу в тригонометрическом виде, используя основное логарифмическое тождество (1 = sin² x + cos² x), разделим почленно числитель на знаменатель, получим табличные интегралы:

 

=

 

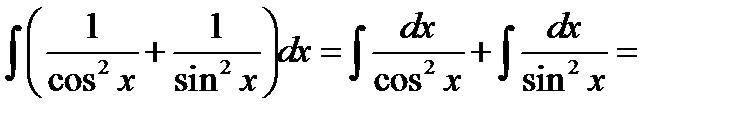
Таблица 3. Таблица основных интегралов
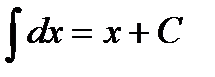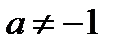
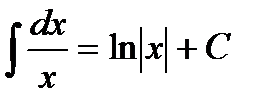
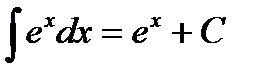