Пусть задана некоторая функция y = f (x). Выберем в области определения функции два произвольных значения аргумента х и х 1. Обозначим за Dх разность между двумя значениями аргумента D х = х 1 – х, (т.е х 1 = х +D х).
Замечание. D х может быть как больше нуля, если х 1 > х, так и меньше нуля, если х 1 < х.
Вычислим значения функции в этих точках y = f (x) и y 1= f (x 1).
Приращением функции D f (x) называется разность между двумя значениями функции
D f (x) = f (x 1) - f (x) = y 1 – y или D f (x) = f (х + D x) – f (x).
Если при D х ® 0 существует конечный предел отношения приращения функции к вызвавшему его приращению аргумента, то функция f (x) называется дифференцируемой в точке х, а значение предела называется производной от функции f (x) в точке х и обозначается
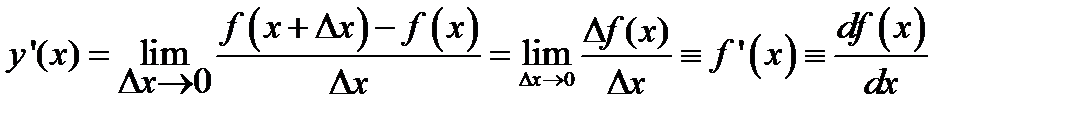
(2.1)
Производная - это функция от того же аргумента, что и f (x). Операцию вычисления производной называется дифференцированием функции.
Геометрический смысл производной. Если изобразить на рисунке график функции f (x), отметить точки х и х 1 = х + D х, то МС = D х, NC = D f (x). Величина отношения
(2.2)
равна тангенсу угла наклона секущей MN к оси абсцисс (см. рис.2.1).
Если Dх ® 0, то точка N стремится по графику функции к точке M, секущая MN стремится занять положение касательной МК к графику функции f (x) в точке M, угол наклона секущей α стремится к углу наклона касательной φ. Сравнивая формулы (2.1) и (2.2) мы можем сказать, что значение производной f ¢(x) в точке х равно тангенсу угла наклона касательной к графику y = f (x) в точке М с координатами (х, f (x)).
Уравнение касательной в точке М
,
уравнение нормали (угловой коэффициент нормали равен 
)
,
Рис. 2.1. Геометрический смысл производной
Замечание. В механике производная от пути по времени есть скорость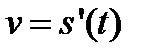 
Правила дифференцирования.
1. Производная постоянной С равна нулю
(C)` = 0 (2.3)
2. Производная линейной комбинации функций f 1 (x) и f 2(x)
у (х) = с1f1 (x) +c2f2 (x), (2.4)
где с1 и c2 произвольные постоянные, равна линейной комбинации производных
у ¢(x) = (с1f1 (x) +c2f2 (x)) ¢ = с1f1 ¢ (x) +c2f2 ¢ (x). (2.5)
Действительно, вычислим приращение функции D у (x).
Для этого выберем в области определения функции два произвольных значения аргумента х и х 1. Вычислим соответствующие значения функции у (x 1) и у (x) и найдем ее приращение.
D у (x) = у (x 1) - у (x) = (с1 f 1(x 1) + с2 f 2(x 1)) - (с1 f 1(x) + с2 f 2(x)).
Сгруппируем отдельно слагаемые содержащие f 1 (x) и f 2(x) и вынесем за скобки константы с1 и с2. Выделим приращения функций f 1 (x) и f 2(x)
D у (x) = (с1 f 1(x 1) - с1 f 1(x)) + (с2 f 2(x 1) - с2 f 2(x)) = с1 (f 1(x 1) - f 1(x)) +
(2.6)
+ с2 (f 2(x 1) - f 2(x))= с1 D f 1(x) + с2 D f 2(x 1).
Подставим приращение функции D у (x) (2.6) в формулу (2.1) (определение производной) и учтем правила вычисления пределов:
предел суммы равен сумме пределов,
постоянный множитель можно вынести за знак предела.
Тогда
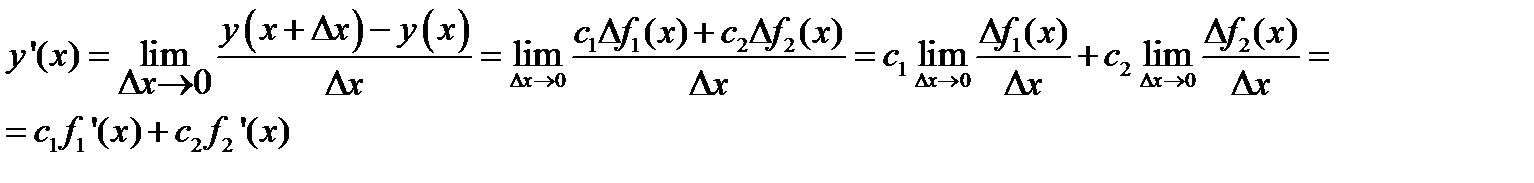
Следствие. Постоянный множитель С можно вынести за знак производной
(С у (x)) ¢= С у ¢(x).
3. Производная произведения функций у (x) = f (x) 
g (x) вычисляется по правилу: произведение производной от первой функции на неизменную вторую плюс произведение производной от второй функции на неизменную первую
у (x)’ = (f (x)g(x))¢ = f ¢(x) g (x) + f (x) g¢(x). (2.7)
Правило можно обобщить на случай производной произведения n функций
(f 1(x) 
f 2(x) 
.. …. … 
f n(x))¢ =
= f 1(x)¢ 
f 2(x) 
…. 
f n(x)+ f 1(x) 
f 2(x)¢ 
…. 
f n(x)+….+ f 1(x) 
f 2(x) 
….. 
f n(x)¢
4. Производная частного двух функций 
вычисляется по правилу
(2.8)
Пример.
1. (6 sin x - 2 ln x)¢ = (6 sin x)¢ - (2 ln x)¢ = 6 (sin x)¢ - 2 (ln x)¢ = 6 cos x - 
В табл. 1 приведены производные основных элементарных функций. В табл. 2 основные правила дифференцирования.
Дифференцирование сложной функции. Пусть дифференцируемая функция g (x) является аргументами другой функции f (x). В этом случае говорят о сложной функции у (x) = f (g (x)) или суперпозиции функций f и g.
Вычислим производную сложной функции. Найдем приращение функции D у (x). Для этого выберем в области определения функции два произвольных значения аргумента х и х 1 = x + D x. Вычислим соответствующие значения функции g (x + D x) и g (x) и найдем ее приращение
D g (x) = g (x + D x) - g (x) 
g (x + D x) = g (x) + D g (x).
Аналогично найдем значения функции f (g (x + D x)) и f (g (x)). Тогда
D f = f (g (x +D x)) – f (g (x)) = f (g (x) + D g (x)) – f (g (x)). (2.9)
Подставим выражение (2.9) в (2.1). Умножим и разделим на D g (x) и сгруппируем сомножители. Тогда производная сложной функции
(2.10)
2. (lnx∙cosx)' = 
∙cosx - lnx∙sinx.
3. 
В компактной форме производную от сложной функции можно записать так
Табица 1. Производные основных элементарных функций
Производная степенной функции:
 ,  .
|
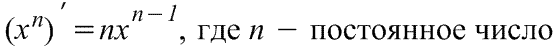Производная экспоненциальной функции:
 ,  ,
|
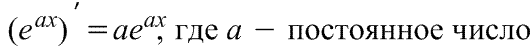Производная сложной экспоненциальной функции:
 .
|
Производная логарифмической функции:
 ,  .
|
Производная сложной логарифмической функции:  .
|
Производная синуса:  .
|
Производная косинуса:  .
|
Производная арксинуса:;
 
|
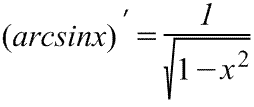
Производная арккосинуса:
 ;  .
|
Производная тангенса:  .
|
Производная котангенса:  .
|
Производная арктангенса:,
 ; 
|
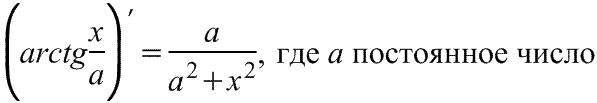
Производная арккотангенса:;
  .
|
(2.11)
Например: у = ln (sin (x 2)). Эта сложная функция состоит из следующих отдельных функций: f = ln g, g = sinh, h = x 2. При этом
Тогда
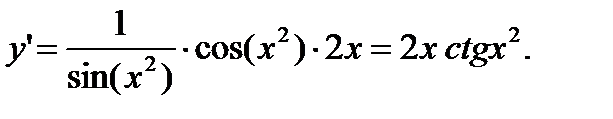
Таблица 2. Правила дифференцирования
| Производная произведения (функции) на постоянную: | 
|
| Производная суммы (функций): | 
|
| Производная произведения (функций): | 
|
| Производная частного (функций): |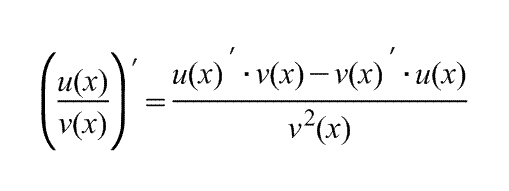 
|
| Производная сложной функции: | 
|
Пример. Пользуясь формулами дифференцирования, найти производные следующих функций:
.
Решение.
1. 
2. 
есть сложная функция 
, где 
.
Производная сложной функции имеет вид 
.
Следовательно,
.
- сложная функция 
, где 
, а 
,
.
Пример 2. Составить уравнение касательной и нормали к кривой 
в точке 
.
Решение. Уравнение касательной , к кривой в точке 
. Здесь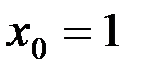 
, 
. Для определения углового коэффициента касательной 
находим производную
, 
.
Подставляя значения 
в уравнение, получим
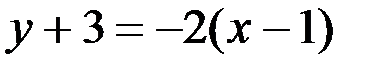или 
.
Уравнение нормали или 
. Раскрыв скобки получим 
.
