Изображение окружности. Пусть на плоскости П' задана окружность S (O', R). Спроектируем ее параллельно прямой т на плоскость П. В этом случае проектирующая прямая опишет цилиндрическую поверхность, которая пересекает плоскость П по эллипсу (рис. 4).
Значит, параллельной проекцией окружности на плоскость П служит эллипс. На основании свойств параллельной проекции можно утверждать, что проекция центра окружности служит центром симметрии эллипса. Центр симметрии эллипса называется центром эллипса. Отрезок, соединяющий две точки эллипса, называется его хордой.
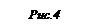
|
Итак, взаимно перпендикулярные диаметры окружности проектируются в сопряженные диаметры эллипса. Эллипс имеет только два взаимно перпендикулярных сопряженных диаметра, которые лежат на осях его симметрии. Эти диаметры называются большой и малой осями эллипса.
Касательная l ' к окружности в точке А' параллельна диаметру [ С'D' ], сопряженному диаметру [ А'В' ]. Она спроектируется в прямую l, которая проходит через точку А, принадлежащую эллипсу, и параллельна диаметру [ СD ], сопряженному диаметру [ АВ ].
Такая прямая называется касательной к эллипсу в точке А. Так как подобие плоскости П переводит эллипс в эллипс и сохраняет отношение длин параллельных отрезков, то изображением окружности является произвольный эллипс, причем перпендикулярные диаметры окружности изображаются сопряженными диаметрами этого эллипса.
Задача. Дано изображение окружности в виде эллипса. Построить изображение двух ее взаимно перпендикулярных диаметров.
Решение.
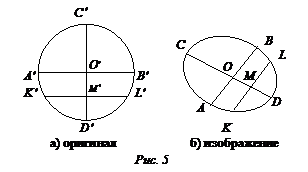 Рассмотрим два перпендикулярных диаметра [
Рассмотрим два перпендикулярных диаметра [ 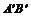 ] и [
] и [ 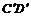 ] окружности (рис. 5а) оригинал). Построим хорду
] окружности (рис. 5а) оригинал). Построим хорду 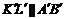 . Параллельное проектирование сохраняет параллельность прямых и отношение отрезков одной прямой. Отсюда вытекает
. Параллельное проектирование сохраняет параллельность прямых и отношение отрезков одной прямой. Отсюда вытекает
свойство искомых диаметров эллипса: каждый из этих диаметров делит пополам хорды, параллельные другому диаметру. Пользуясь этим свойством, выполним построение. Построим произвольный диаметр [ АВ ] эллипса (рис. 5б изображение) и параллельную [ AB ] хорду [ KL ]. Затем строим середину М этой хорды и проводим через М и О диаметр CD. [ AB ] и [ CD ] – диаметры эллипса, изображающие перпендикулярные диаметры окружности. Такие диаметры эллипса называются сопряженными.
Контрольные вопросы и упражнения
1. Треугольник АВС является проекцией треугольника А 1 В 1 С 1. В треугольнике А 1 В 1 С 1 проведены из вершины биссектриса, медиана и высота. Будут ли проекции этих отрезков являться биссектрисой, медианой и высотой треугольника АВ С?
2. Дано изображение равнобедренного треугольника в виде разностороннего треугольника. На этом изображении постройте:
1) изображение биссектрисы угла при вершине;
2) изображение перпендикуляра к основанию, проведенного через середину боковой стороны.






