План:
§ 1. Система уравнений. Совокупность уравнений
§ 2. Неравенства с одной переменной
§ 3. Теоремы о равносильных неравенствах
Система уравнений. Совокупность уравнений
Определение. Системо й (совокупностью) уравнений f (х, у) = 0и F (х, у) = 0 называют конъюнкцию (дизъюнкцию) этих уравнений и записывают
(1) 
Мы знаем, что множество истинности конъюнкции (дизъюнкции) двух предикатов является пересечением (объединением) множеств истинности этих предикатов. Точно также множество решений системы (1) (совокупности (2)) является пересечением (объединением) множеств решений уравнения f (х, у) = 0 и уравнения F (х, у) = 0.
Рассмотрим способы решения систем уравнений с двумя переменными (способы решения совокупности аналогичны).
Геометрический способ решения состоит в следующем: начертим графики уравнений f (х, у) = 0 и F (х у) = 0и найдем точки их пересечения. Координаты этих точек и будут искомыми значениями х и у.
П р и м е р.
Решить графически систему: 
Графиком уравнения
|
|
|
|
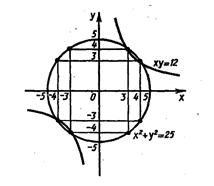
Рис. 1
является окружность с центром в начале координат и радиусом, равным 5. Графиком уравнения ху = 12 является гипербола 
. Построив графики в одной системе координат (рис. 1), найдем координаты точек А, В, С, D пересечения окружности и гиперболы: А (4; 3), В (3; 4), С (–4; –3), D (–3; –4). Значит, решения заданной системы таковы: (4; 3), (3; 4), (–4; –3), (–3; –4)
Из школы известны алгебраические способы решения систем уравнений с двумя неизвестными:
а) способ подстановки состоит в том, что:
1) из одного уравнения мы находим выражение одного из неизвестных, например х, через известные величины и другое неизвестное у;
2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное у;
3) решаем полученное уравнение и находим значение у;
4) подставляя найденное значение у в выражение неизвестного х, найденное в начале решения, получаем значение х.
Например,
Решаем второе уравнение:
5(46 + 3 у) + 48 у = 104.
230 + 15 у + 48 у = 104. 63 у = –126 Þ у = –2.
Находим х = 5. Решение. (5, –2).
б) способ алгебраического сложения состоит в том, что:
1) обе части одного уравнения умножают на некоторый множитель. Эти множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну и ту же абсолютную величину;
2) складываем (или вычитаем) эти уравнения друг с другом;
3) решаем полученное уравнение с одним неизвестным;
4) другое неизвестное можно найти тем же приемом, но обычно проще подставить его в любое из данных уравнений и решить получившееся уравнение с одним неизвестным.
