Свойства параллельных проекций

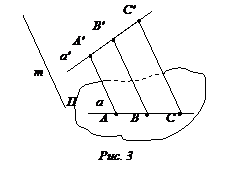
Свойство 1. Изображение прямой линии есть прямая или точка (рис. 3).

Предположим, что прямая а' – не проектирующая. Возьмем на ней любые точки А', В', С',... и проведем через них проектирующие прямые. Эти прямые лежат в одной плоскости (проходящей через а' и параллельной т). Пересечение этой плоскости с плоскостью П есть прямая. Заметим, что плоскость, параллельная направлению проектирования т, называется проектирующей плоскостью.

Если прямая а' – проектирующая, то все ее точки имеют одно и то же изображение, т.е. вся прямая изображается точкой.

Свойство 2. Параллельные прямые изображаются параллельными прямыми (в частности, может быть, совпавшими) или каждая одной точкой (рис. 4).

Предположим. что параллельные прямые а', в', с',..., не проектирующие. Проходящие через них проектирующие плоскости a, b, 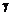,..., параллельны между собой (а может быть и совпадают) и, следовательно, пересекают плоскость П по параллельным прямым а, в, с,..., (в частности – совпадающим). Если же параллельные прямые проектирующие, то они изображаются отдельными точками.

Свойство 3. Отношение, в котором точка отрезка делит этот отрезок, в изображении и в оригинале одинаково, т.е. 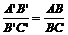 (*)(рис. 5).

Проведем через точку В' прямую, параллельную АС. Треугольники В'А'А ₁, и В'С'С₁ подобны. Из подобия треугольников следует пропорция (*).

Изображение, которое строится без учета расположения оригинала относительно чертежа, называется свободным изображением. При изучении, в иллюстративной практике и в большинстве инженерных приложений применяются свободные изображения. Мы всегда чертим какой-нибудь куб или какой-нибудь шар. Чтобы свободное изображение было правильным, нужно, строя его, руководствоваться некоторыми правилами.

Определение. Изображением данной фигуры называют любую фигуру, подобную параллельной проекции данной фигуры.

Согласно этому определению изображение по методу параллельного проектирования может быть получено в результате выполнения двух операций.

1. Все точки фигуры проектируются параллельно проектирующей прямой на плоскость проекций.

2. Полученная фигура подвергается подобному преобразованию.

Фигура, полученная в результате выполнения этих двух операций, и называется изображением оригинала.

Вторая операция имеет целью придать чертежу удобные размеры, чтобы он поместился на классной доске или на листе бумаги. Разумеется, в тех случаях, когда размеры проекции нас устраивают, второй операции может и не быть, или для общности рассуждений ее можно рассматривать как тождественное преобразование.

В стереометрии часто приходится изображать, пространственные фигуры, содержащие различные плоские элементы.

Теория изображения плоских фигур основана на следующих двух теоремах (правилах, упомянутых в § 2).

Теорема 1. Любой данный треугольник может быть изображен произвольным треугольником.

Доказательство. Пусть дан треугольник А'В'С'. Через прямую (А'В') проведем плоскость П не параллельную плоскости ∆ А ¢ В ¢ С ¢ и примем ее за плоскость проекций. Зададим в плоскости П произвольный треугольник МРN. В плоскости П построим на отрезке [ А'В' ] ∆А'В'С подобный треугольнику МРN (рис.6). Если спроектировать ∆А ¢ В ¢ С ¢ на плоскость П параллельно прямой (С'С), то получим ∆А ¢ В ¢ С. Отсюда, согласно определению, следует, что изображением данного треугольника А'В'С' может служить произвольный треугольник МРN.

Теорема 2. Если дано изображение треугольника А'В'С', то тем самым однозначно определено изображение каждой точки, принадлежащей плоскости этого треугольника.

Доказательство. Пусть треугольник А'В'С' – оригинал, а ∆АВС – его изображение (рис. 7).

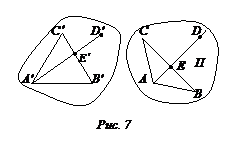Возьмем в плоскости треугольника А'В'С' произвольную точку D' и проведем прямую (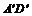). Предположим что (А'D') || (В'С').

Пусть { Е' } = (А'D') (В'С') (безразлично, находится ли Е' внутри отрезка В'С' или на его продолжении). Изображение Е точки Е' можно найти, воспользовавшись соотношением: . Положение точки D на прямой АЕ определяется из пропорции 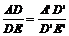. Если (A ¢ D ¢)||(В ¢ С ¢), то (АD) || (ВС) и .

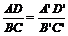Итак, в любом из рассмотренных случаев положение точки D на плоскости П определено.

Из доказанной теоремы вытекает практическое правило для построения изображений плоских фигур.

При построении изображения Ф плоской фигуры Ф' три ее точки, не принадлежащие одной прямой, можно изобразить тремя произвольными точками, не принадлежащими одной прямой. На этом произвол в изображении Ф заканчивается, изображения остальных точек оригинала Ф' вполне определены. В качестве примера рассмотрим изображения некоторых плоских фигур.

Замечание. При параллельном проектировании фигур обращают внимание лишь на начальное (оригинал) и конечное (изображение) положение проектируемой точки, отвлекаясь от ее промежуточных положений. Поэтому нет необходимости каждый раз изображать вместе с фигурой плоскость проекций и проектирующую прямую.

Контрольные вопросы и упражнения

1. Дан перечень фигур:

1) точка;         2) прямая; 3) отрезок;

4) луч;        5) угол;      6) плоскость.

Какие фигуры могут получиться при проектировании каждой из данных фигур? При выборе ответов пользуйтесь этим же перечнем.

2. Даны точки А ₁, В ₁ и их проекции А, В на плоскость П. Постройте точку пересечения прямой А ₁ В ₁ с плоскостью П.

3. Даны точки А ₁, В ₁, С ₁, не принадлежащие прямой, и их проекции А, В, С на плоскость П. Постройте линию пересечения плоскостей А ₁ В ₁ С ₁ и П.