Методы решения задач на построение

К решению задач средней или повышенной трудности часто привлекают некоторые специальные методы. Три метода являются основными при решении геометрических задач на построение:

а) метод геометрических мест,

б) метод геометрических преобразований,

в) алгебраический (аналитический) метод.

Рассмотрим каждый из этих методов на конкретных примерах.

а) Метод геометрических мест. Этот метод состоит в следующем. Пусть требуется найти некоторую точку, удовлетворяющую двум независимым условиям. Геометрическое место точек, удовлетворяющих только первому условию, есть некоторая фигура Ф ₁, а геометрическое место точек, удовлетворяющих только второму условию, есть некоторая фигура Ф ₂. Ясно, что обоим условиям удовлетворяет каждая точка пересечения фигур Ф ₁ и Ф ₂, а всякая точка, не принадлежащая пересечению этих фигур, не удовлетворяет хотя бы одному из этих условий. Каждая точка фигуры 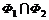 дает возможность найти некоторое решение задачи.

Решим задачу методом геометрических мест.

Задача 1. Построить треугольник АВС по сторонам ВС = а, АС = b и углу АВС = b при основании.

Решение. Анализ. Пусть ∆ АВС уже построен, тогда положение вершин В и С можно считать известным, остается найти вершину А (рис. 1). Выясним свойства точки А. Во-первых, точка А принадлежит лучу [ ВА) (А Î[ ВА)), т.к. дан АВС = b). Во-вторых, точка А удалена от точки С на данное расстояние b, т.е. точка А принадлежит окружности S с центром в точке С и радиусом b (А Î S (С, b)).

Вывод: если точка А существует, то она является точкой пересечения луча [ ВА) с окружностью S (С, b). План построения очевиден.

Построение. Возьмем данные отрезки а, b и угол b (рис. 2). Построение выполним по шагам:

1) построим отрезок [ ВС ] = а;

2) на отрезке [ ВС ] построим угол Ð АВС = b;

3) построим окружность S с центром в точке С и радиусом b;

4) найдем точку пересечения луча [ ВА) и окружности S, обозначим ее А (рис. 3).

 

 

	Рис. 2
			Рис. 3

 

Доказательство. В АBС содержатся данные элементы: сторона [ ВС ] = а, [ AC ] = b и АВС = b. Значит, AВС – искомый.

Исследование. Его обычно выполняют по шагам построения.

1) заданный отрезок можно построить с точностью до расположения на плоскости;

2) угол ABC можно отложить по разные стороны [ ВС);

3) шаг выполним единственным образом;

4) если получится одна точка пересечения, то задача имеет одно решение (получится один треугольник), если получится две точки пересечения, то задача имеет два решения (получится два разных треугольника), если нет точки пересечения, то задача при выбранных данных не имеет решения.

б) Метод геометрических преобразований при решении задач на построение применяется, когда фигуры обладают какими-либо особыми свойствами (например, центральные, симметричные и т.п.) или когда при решении этих задач могут быть полезными дополнительные построения.

В зависимости от того, какое именно геометрическое преобразование выбрано, говорят о той или иной разновидности метода геометрических преобразований: о методе параллельного переноса, о методе гомотетии и т.п.

При построении многоугольников, не являющихся треугольниками, выгодно сблизить данные или искомые фигуры. Такое сближение позволяет часто свести задачу к построению некоторого треугольника. Сближение фигур удобно осуществить посредством параллельного переноса.

Решим задачу методом геометрических преобразований.

 

 

Задача 2. Построить трапецию по заданным ее сторонам.

Решение. Анализ. Пусть трапеция АВСD построена,

[ ВС ] = а, [ АD ] = b, [ АВ ] = с, [ СD ] = d (рис. 4). Выполним параллельный перенос, определяемый вектором . Тогда сторона [ СD ] перейдет в [ ВD' ]. АВD ' можно построить по трем сторонам                с, d, b – а (b > а). Затем продолжим отрезок [ АD' ] на [ DD' ] = а. Через точку В проведем прямую, параллельную (АD) и на ней отложим отрезок [ ВС ] = а. Соединим точки С и D. Полученная трапеция АВСD – искомая. План построения очевиден.

Построение. Выберем четыре отрезка: а, b, с, d, будем считать, что а и b – основания трапеции   (b > а), с, d – боковые стороны (рис. 5).

 

                 b

   a

         c

      d

 

   Рис. 5                                                      Рис. 6

Построение выполняется по шагам:

1) построим ∆ АВD ¢ по трём сторонам c, d, b – а;

2) выполним параллельный перенос отрезка [ ВD ¢] на вектор  (), тогда точка В перейдёт в точку C, точка D ¢ в точку D.

Четырехугольник АВСD – искомая трапеция (рис. 6).

Доказательство. В четырёхугольнике АВСD: [ ВС ] || [ АD ], значит, АВСD – трапеция, в которой [ ВС ] = а, [ АD ] = b, ([ АD ] = b – а + а), [ АВ ] = с, [ ВD ¢] = [ СD ]= d.

Исследование.  можно построить по трем сторонам, если
с – d < b – а < c + d (условие существования треугольника). При этом условии однозначно выполнимы и все остальные шаги построения. Если с – d < b – а < c + d не выполняется, то задача не имеет решения при выбранных данных.

в) Алгебраический (аналитический) метод решения задач на построение обычно применяется, когда требуется построить отрезок х, который задан уравнением вида х = f (а, b,..., с), где а, b,..., с – заданные отрезки. Сущность метода заключается в следующем. Решение задачи на построение сводится к построению некоторого отрезка (или нескольких отрезков). Величину искомого отрезка выражают через величины известных отрезков с помощью формулы. Затем строят искомый отрезок по полученной формуле.

Рассмотрим примеры (I-IV).

I. x = , где n Î N, это задача на деление данного отрезка на равные части и решается она по известной из школьного курса геометрии теореме Фалеса.

II. х =   – задача на построение отрезка, который является четвертым пропорциональных трех данных отрезков.

Перепишем уравнение в виде . Полученная пропорция позволяет решить задачу построением подобных (гомотетичных) треугольников.

III. х =   – задача на построение среднего пропорционального (среднего геометрического) отрезка между данными отрезками. Из школьного курса геометрии известно, что высота прямоугольного треугольника, опущенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.

Отсюда план построения отрезка x таков: сначала построим окружность на отрезке а + b, как на диаметре. Множество точек этой окружности – есть геометрическое место точек, являющихся вершинами прямоугольных треугольников с гипотенузой а + b. Среди этих прямоугольных треугольников находим тот, высота которого опущенная из вершины прямого угла попадает в точку пересечения отрезков а и b, отложенных на одной прямой.

Построение (рис. 7).

1) Отложим отрезки [ АВ ] = а и [ ВС ]= b на одной прямой, так, что

[ АВ ]+ [ ВС ]= а + b.

2) Найдём середину отрезка [ АС ]. Обозначим эту точку О.

3) Проведём окружность с центром в точке О и радиусом равным [ OС ].

4) Проведём перпендикуляр к [ АС ] из точки В.

5) D, D ¢ – точки пересечения проведённого перпендикуляра и окружности. Искомый отрезок x = [ ВD ]. ([ ВD ¢] = [ ВD ]).

 

IV. х = , х =  при а > b – эти задачи на построение решаются по теореме           Пифагора.