Определение. Дробно-линейной функцией называется функция вида y = 
, где коэффициенты a, b, c, d – действительные числа.
Область определения этой функции есть всё множество действительных чисел, кроме числа равного – 
. Множество значений функции есть множество всех действительных чисел, кроме 
.
Эта функция представляет собой частное двух линейных функций. Дробно-линейная функция сводится к линейной функции при
с = 0, а d ¹ 0 и к постоянной при ad = bc. При a = d = 0, с ¹ 0 из дробно-линейной функции получается обратная пропорциональная зависимость, выражаемая формулой 
, где 
.
Покажем, что график дробно-линейной функции
y = 
(1)
при с ¹ 0 и ad – bc ¹ 0 получается из графика обратной пропорциональности параллельным переносом осей координат.
Преобразуем сначала уравнение
.
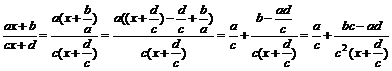Для построения графика используем параллельного переноса системы координат.
Значит, для построения графика заданной функции надо перенести начало координат в точку О ¢ (– ; 
и построить график обратной пропорциональности y ¢ = 
, где k = 
.
П р и м е р. Постройте график функции 
.
Найдем координаты нового начала координат О ¢ = 
, получим О ¢ = (1; 1). Подсчитаем значение 
, получим k = 1, тогда в новой системе координат x ¢ O ¢ y ¢ 
.
Построим график этой функции в системе координат x ¢ O ¢ y ¢ (рис. 3).
Рис. 2
Лекция 6. Тема: Уравнения и неравенства
План:
§ 1. Числовые выражения
§2. Числовые равенства. Свойства числовых равенств
§ 3. Числовые неравенства. Свойства числовых неравенств
§ 4. Выражения с переменными
Основная задача современной алгебры – это изучение алгебраических операций и их свойств. С другой стороны, алгебра (особенно элементарная) – это учение о тождественных преобразованиях, о решении уравнений, неравенств, их систем и совокупностей.
Числовые выражения
Определение. 1) Каждая отдельная цифра или буква (латинского алфавита) – выражение. Эти выражения называют элементарными. 2) Если А и В – выражения, то (А) + (В), (А) – (В), (А) · (В), (А): (В) – выражения. 3) Других выражений, кроме тех, которые могут быть получены в соответствии с пунктами 1) и 2) нет.
Если к этим четырём арифметическим действиям добавить действие возведение в степень и извлечение корня, можно получить более сложные выражения.
Для сокращения записи условились не заключать в скобки, если несколько выражений складываются и вычитаются, причём эти операции выполняются по порядку слева направо. Точно также, если делят или умножают несколько чисел.
Наконец, условились выполнять сначала действия второй ступени (умножение и деление), а потом – первой (сложение и вычитание).
Если задано выражение со скобками, то сначала выполняют действия в них. В выражениях, образованных в соответствии с данным определением, должно содержаться четное число скобок, столько же правых, сколько левых.
Определение. Выражение, не содержащее букв (переменных), т.е. состоящее из одних цифр, знаков операций и (возможно) скобок, называют числовым выражением.
П р и м е р ы. 3; (8 + 1) · (14 + 15);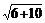 
– числовые выражения.
Каждому числовому выражению соответствует числовое значение (Зн), причем
Зн (А ± В) = Зн (А) ± Зн (В); Зн (А · В) = Зн (А) · Зн (В); Зн (А: В) = Зн (А): Зн (В).Если Зн (В) = 0,то Зн (А: В) не существует. Например, числовые выражения 8: (4 – 4) и (6 – 6):(3 – 3) не имеют числовых значений.
С числовыми выражениями учащиеся начальных классов знакомятся очень рано. Сначала это выражения вида 2 – 1; 1 + 1; 2 – 1; 3 + 2. Позже появляются более сложные числовые выражения.
