График квадратичной функции

Многие физические зависимости выражаются квадратичной функцией, например, камень, брошенный вверх со скоростью V ₀, находится в момент времени t на расстоянии  от земной поверхности (здесь g –ускорение свободного падения); количество тепла Q, выделяемого при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой Q = RI ².

Определение. Квадратичной функцией называется функция вида у = ах² + bх + с, где коэффициенты а, b, с – действительные числа.

Область определения этой функции есть все множество действительных чисел, т.е. функция задана в интервале (–¥, +¥), множество значений функции есть также интервал (–¥, +¥). Простейший частный случай квадратичной функции есть функция y = ax ², график ее называется параболой. У всех этих парабол вершины находятся в начале координат; при a > 0 это наинизшая точка графика (наименьшее значение функции), а при a < 0, наоборот, наивысшая точка графика (наибольшее значение функции). Ось Оу есть ось симметрии каждой их этих парабол. При a > 0 парабола направлена вверх, при a < 0 – вниз.

График функции y = ax ² + bx + c отличается от графика y = ax ² лишь своим положением и может быть получен просто перемещением кривой на чертеже.

Применим результаты предыдущих параграфов о преобразованиях графиков функций к построению графика квадратичной функции. Преобразуем сначала уравнение y = ax ² + bx + c.

y = ax ² + bx + c =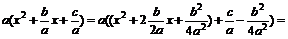

. Получили уравнение вида y = a (x – a)² + b, здесь a = – , b = .

Для построения графика используем способ параллельного переноса системы координат.

Перенесем начало координат в точку O' (a, b) и построим новую систему координат. Тогда данное уравнение примет вид у' = ах '² – это уравнение получилось уже в новой системе координат х'O'у', которая получена из хОу путём параллельного переноса системы координат в точку O' (a, b).

В уравнении  сделаем такую замену:

x ¢ = x – a

y ¢ = y – b,

тогда данное уравнение примет вид у' = ах '² – это уравнение получилось уже в новой системе координат х'O'у', которая получена из хОу путём параллельного переноса системы координат в точку O' (a, b).

Построение графика будем выполнять следующим образом:

1) перенесем начало координат в точку O'(a, b), где

a = – , b = ;

2) построим в новой системе координат параболу  у' = ах '²;

3) если а < 0, то график отражаем симметрично относительно оси О' х.

П р и м е р. Построить график функции y = 2 x² – 4 x +1

Преобразуем это уравнение:

y = 2(x ² – 2 x +1) – 1 = 2(x – 1)²– 1.

1) Перенесем начало координат в точку О' (1; –1) и построим новую систему координат ;

Рис. 28

2) построим у' = 2  в новой системе координат (рис. 1).

§ 2. Обратная пропорциональность и ее график

Определение. Функцию вида   называют обратной пропорциональностью. Говорят также, что в этом случае величина  обратно пропорциональна величине х.

Произведение у · х принимает одно и тоже значение k, его называют коэффициентом обратной пропорциональности.

Обратно пропорциональная зависимость связывает, например, давление газа р и его объем V при постоянной температуре, так как по закону Бойля – Мариотта pv = сопst. В случае равномерного движения при прохождении заданного пути S время движения t обратно пропорционально скорости v, т.е. .

Графики функций  при различных значениях k (k ¹ 0)– это кривые, называемые равнобочными гиперболами.

Изучим свойства функции  и построим ее график. Функция  определена на всей числовой прямой, кроме х = 0.Если k > 0,то функция убывающая, при k < 0 – возрастающая. Убедимся в этом.

Пусть k > 0,тогда при х ₂ > х ₁, имеем у ₂ < у ₁. Действительно, 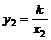, откуда .

Пусть теперь k < 0,тогда при х ₂ > х ₁, имеем .

При возрастающих положительных значениях х значения  уменьшаются, причем, чем больше значение х, тем ближе значение у кнулю. Эта часть графика располагается в I четверти.     Чтобы получить часть графика при отрицательных значениях х, заметим, что вместе с точкой              А (х ₀, у ₀) график функции содержит точку А' (– х ₀, – у ₀). В самом деле, если . Но точки А и А' симметричны относительно начала координат. Поэтому график функции  симметричен относительно начала координат. То есть при отрицательных х часть графика располагается в III четверти.

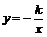График функции  получается из графика функции  в результате симметрии относительно оси абсцисс и будет тогда располагаться в II и IV четвертях. На рис. 1 изображены графики функций   (сплошной линией) и  (штриховой линией).

Когда х стремится к бесконечности (неограниченно увеличивается), график функции  неограниченно приближается к оси абсцисс, но не достигает ее. Ось абсцисс называют горизонтальной асимптотой этой кривой. Когда х стремится к нулю (неограниченно уменьшается), график функции  неограниченно приближается к оси ординат, но не достигает ее. Ось ординат называют вертикальной асимптотой этой кривой. А сама кривая, являющаяся графиком обратной пропорциональности, называется гиперболой.