Определение. Два числовых выражения А и В, соединенных знаком «>» (больше) или «<» (меньше) образуют числовое неравенство. Неравенства А > B и C > D (или А < B и C < D) называются неравенствами одинакового смысла (знака), а неравенства А > B и C < D (или А < B и C > D) – неравенствами противоположного смысла.
С логической точки зрения числовое неравенство представляет собой высказывание И или Л. Например: 12 · 3 > 10 – И; 12 + 14 < 15 – Л. К числовым неравенствам применимы логические операции, в частности, можно образовать конъюнкцию и дизъюнкцию числовых неравенств:
(2 < 3) Ù (5 < 3) – Л; (3 < 5) Ú (1 + 1 > 3 + 1) – И.
Неравенство А £ В является дизъюнкцией равенства А = В и неравенства А < В,
т.е. А £ В Û (А < B) Ú (А = В), например,
(2×4 + 15) × 2 £ 35 + 19 – И.
Двойное неравенство А < В < С является конъюнкцией неравенств А < В и В < С. Оно истинно в том и только в том случае, когда истинны оба эти неравенства. Например, рассмотрим конъюнкцию неравенств (25 < 18 + 17 × 2) Ù (18 + 17 × 2 < 100). Её можно переписать в виде двойного неравенства: 25 < 52 < 100. Прежде всего отметим, что неравенство («<», «>») обладает свойствами отношения строгого порядка:
1°. Антирефлексивность (" А) [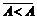 
],
(" А) [ 
];
2°. Антисимметричность (" А, В)[ А < В Þ 
],
(" А, В)[ А > В Þ 
];
3°. Транзитивность (" А, В, С) [ А < В Ù В < С Þ А < С ],
(" А, В, С) [ А > В Ù В > С Þ А > С ].
В свойствах 1°–3° А, В, С –любые числовые выражения.
Кроме приведенных выше свойств 1°–3° в качестве основных примем следующие свойства для любых двух действительных чисел x и y:
1) 
, причем имеет место одно и только одно из отношений либо x = y,либо x > y, либо y > x;
2) (" х, у)[ x < y Û y – x > 0];
3) (" х, у)[ x > 0 Ù y > 0 Þ x + y > 0 Ù x × y > 0].
Заметим, что неравенство y > x эквивалентно неравенству x < y – оба неравенства одновременно истинны или ложны. Знаки «>» и «<» взаимно обратны.
Из указанных выше свойств 1)-3) можно вывести для любых числовых выражений x, y, a, в все остальные свойства числовых неравенств.
1°. (" x, y, a) [ x < y Þ x + a < y + a ].
Доказательство. x < y Û y – x > 0Þ (y + a) – (x + a) = y – x > 0 Þ
Þ x + a < y + a. Точно также x – a < y – a.
2°. (" x, y, a, в) [ x < y Ù a < в Þ x + a < y + в ].
Доказательство. x < y Þ y – x > 0, a < в Þ в – а > 0.
(у – х) + (в – а) = (у +в) – (х +а)> 0 Þ х +а < у +в.
3°. (" х, у, а > 0) [ х < у Þ х · а < у · а ].
Доказательство.
х < у Þ у – х > 0 Þ а (у – х) > 0 Þ ау – ах > 0 Þ ау > ах Û ах < ау.
4°. (" х > 0," у > 0," а > 0," в > 0) [ х < у Ù а < в Þ ах < ву ].
Доказательство. х < у Ù а > 0 Þ (у – х)× а > 0 Û х · а < у · а.
а < в Ù у > 0 Þ ау < ву. (ха < уа) Ù (уа < ву) Þ ха < ув Û ах < ву.
5°. (" х, у)[ х < у Þ –х > –у ].
Доказательство. х < у Þ у – х > 0. у – х = (– х) – (– у) > 0 Þ – х > – у.
6°. (" х, у, а < 0) [ х < у Þ ах > ау ].
Доказательство. х < у Þ 
· х < · у Þ– · х >– · у, т.е. ах > ау.
7°. (" х, у Ù 0 < х < у либо х < у < 0) [ 
< 
].
Доказательство. – = 
, в полученной дроби числитель у – х > 0 и знаменатель х · у > 0, значит > 0 и > .
Выражения с переменными
Наряду с числовыми выражениями рассматривают выражения с переменными. Они определяются также как числовые выражения, только кроме чисел, выражения с переменными содержат и буквы. Например, 2 а + 3 в; 5 х + 18; 4 у – 9 и т. д. Если для каждой буквы указано некоторое множество числовых значений, которые может принимать эта буква, то ее называют числовой переменной.
Определение. Областью определения выражения с переменной называют множество, состоящее из чисел, которые можно подставлять в выражение, т. е. множество чисел, при которых это выражение имеет определенное числовое значение.
Выражение с переменными не является предикатом, т.к. при подстановке вместо букв числовых значений получается не высказывание, а числовое выражение. Значением этого выражения является не истина или ложь, а некоторое число.
Обозначают выражение с переменной А (х), В (х, у) и т. д.
Рассмотрим п р и м е р ы.
1) найти область определения выражения: 
+ 
.
Областью определения является (–¥,1) 
(1, 6) (6, +¥).
2) 
. Область определения этого выражения определяется из неравенства х +10 
0 Þ х –10,т.е. [–10, ¥).
3) если в задаче речь идет о людях, то, составляя выражения с переменной, уже имеют в виду, что областью определения данного выражения с переменной является множество N.
4) Область определения выражения 5 х + 5 у + 10 совпадает с множеством действительных чисел.
Определение. Два выражения с переменными называют тождественно равными, если они принимают одинаковые значения при любых допустимых значениях, входящих в них букв.
Например, выражения (х + у)2и (х 2+ 2 ху + у 2) тождественно равные на множестве R.
Выражения 
и 
тождественно равные на множестве R \{0}.
Основные понятия переменной и выражения с переменной закладываются в начальной школе.
Термины «выражения с переменной», «переменная» здесь не используется. В начальной школе говорят о выражении, содержащем буквы. Такие выражения младшие школьники читают, записывают, подсчитывают значения выражений.
