Физическая постановка задачи формирования граничных условий.

Простейшее формирование граничных условий из экспериментальных данных можно реализовать только в отдельных случаях. Это связано, с одной стороны, с трудностью получения экспериментальных значений, с другой стороны, с тем, что любые экспериментальные данные являются случайными величинами, что вносит серьезные проблемы в численное решение уравнений и ограничивает экстраполяцию и интерполяцию нашей задачи.

На практике, в качестве граничных условий берут известные закономерности поведения уравнений в какой-то области. При этом существуют типовые постановки задач, которые позволяют моделировать процессы, для которых экспериментальных данных не существует вообще.

Одной из типичных постановок, является постановка, когда система на какой-либо из границ находится в стационарном состоянии или, в частном случае, в термодинамическом равновесии.

Стационарные состояния, т. е. такие состояния, в которых параметры, их определяющие, не зависят от времени, играют важную роль в приложениях неравновесной термодинамики. Стационарные состояния могут быть как равновесными, так и неравновесными в зависимости от граничных условий, накладываемых на систему.

До рассмотрения стационарных состояний мы обсудим некоторые свойства состояния механического равновесия. Стоит заметить, что при некоторых условиях, из которых наиболее важным является предположение о постоянстве феноменологических коэффициентов и справедливости соотношений взаимности Онсагера, стационарные состояния являются в то же время состояниями с минимальным производством энтропии, совместимым с внешними воздействиями.

Механическое равновесие

Для случая состояния механического равновесия можно доказать теорему, упрощающую описание некоторых необратимых процессов, в частности явлений диффузии.

Состояние механического равновесия есть состояние, в котором ускорение dv/dt равно нулю. Мы интересуемся такими состояниями механического равновесия, в которых не только ускорения равны нулю, но и пренебрежимо малы градиенты скоростей, а, следовательно, мал и вязкий тензор давлений П.

Для таких состояний уравнение движения (2.19) принимает вид:

0=:-grad p + (1.83)

В ряде важных случаев состояние механического равновесия, описываемое уравнением (1.83), действительно устанавливается за время, значительно меньшее времени, характерного для термодинамических процессов. Таким образом, фактически это состояние достигается уже к началу исследуемых необратимых процессов. Для более общих случаев это утверждение не всегда справедливо: все зависит от конкрет­ной физической ситуации. Можно представить себе, например, осциллирующие системы, в которых ускорение все время отлично, от нуля. Однако, например, для явлений диффузии или термодиффузии в замкнутых сосудах вполне разумно предполагать, что в хорошем приближении состояние механического равновесия, описываемое урав­нением (1.83), быстро реализуется. В диффузионных экспериментах ускорение dv/dt может быть отличным от нуля, например, в том случае, когда молекулярные массы участвующих в процессе компонентов имеют разную величину. Однако это ускорение очень мало и возникающие градиенты давления (если предположить отсутствие внешних сил) также пренебрежимо малы. Налагаемая в начальный момент разность давлений также приведет к появлению ускорений, но они исчезнут вследствие наличия вязкости задолго до того, как процесс диффузии достигнет стационарного состояния. Таким образом, вновь предполагая отсутствие внешних сил F_k, мы можем считать градиенты давления пренебрежимо малыми уже почти в самом начале процесса диффузии.

Для состояния механического равновесия (1.83) Пригожин [6] доказал теорему, согласно которой в выражении для производства энтропии (4.13) массовую скорость v, входящую в определение (2.9) диффузионного потока J_k, можно заменить другой произвольной скоростью v^а.

Доказательство этой теоремы основано на справедливости сле­дующего равенства:

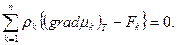(1.84)

Это равенство легко получается, если заметить, что для удельной функции Гиббса

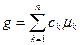(1.85)

имеем

(1.86)

Из (1.85) и (1.86) следует соотношение Гиббса—Дюгема

(1.87)

или

(1.88)

Стационарные состояния

 

Подставляя grad p из уравнения движения (1.83) для случая механического равновесия в последнее соотношение, получаем для стационарных состояний тоже уравнение (1.84).

Таким образом, задачи, связанные с закрепленными границами (балки, колебания различного типа приборов) и с фазовыми переходами, могут иметь в качестве одного из граничных условий уравнение стационарного состояния. На остальных границах можно также указать некоторые типовые положения для постановки граничных условий:

1. Поток на дальних границах равен 0 (или о(u) – «о» малое от функции потока).

2. Поток зеркально отражается от границы (u ₊= u _-).

3. Скорость потока равна нулю (d u /dt=0).

При этом не всегда необходимо ограничивать полную область переменных. Иногда изменение процесса нас интересует на небольшом участке (размеров или времени). В этом случае можно предположить, что какая-либо из границ, в т.ч. время, удалена на бесконечность. Многие уравнения в частных производных при этом имеют аналитические решения, которые получены в стандартной постановке краевых задач для линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Рассмотрим математическую постановку таких краевых задач.