Постановка краевых задач для линейных дифференциальных уравнений второго порядка

Существуют стандартные математические модели для ряда характерных физических процессов, которые сводятся к различным краевым задачам для линейных дифференциальных урав­нений второго порядка.

 

1. Классификация краевых задач. Как было показано в § 1.2, линейное дифференциальное уравнение второго порядка

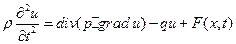(1.89)

описывает процессы колебаний, уравнение

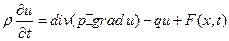(1.90)

описывает процессы диффузии и, наконец, уравнение

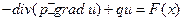(1.91)

описывает соответствующие стационарные процессы.

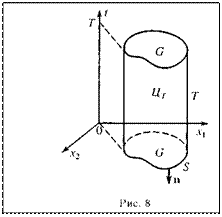
Пусть G Ì Rⁿ область, где происходит процесс, и S - ее граница, которую считаем кусочно-гладкой поверхностью. Таким образом, G есть область изменения аргументов x в уравнении (1.91) – область задания уравнения (1.91). Областью задания уравнений (1.89) и (1.90) будем считать цилиндр Ц_T =G ´ (0,T) высоты T с основанием G. Его граница состоит из боковой поверхности S ´[О,T] и двух основании: нижнего 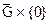и верхнего (рис. 1.3).

Будем предполагать, что коэффициенты r, p, q уравнений (1.89) - (1.91) не зависят от времени t; далее в соответствии с их физическим смыслом будем считать, что

 

r(x) > 0, p(x) > 0, q(x)³ 0 при

 

Наконец, в соответствии с математическим смыслом уравнений (1.89)-(1.91) необходимо считать, что

Рис. 1.3

При этих предположениях согласно классификации §1.3 урав­нение колебаний (1.89) - уравнение гиперболического типа, уравне­ние диффузии (1.90) - параболического типа и стационарное уравнение (1.91) - эллиптического типа. Таким образом, различие в типах рассматриваемых урав­нений тесно связано с различием физи­ческих процессов, описываемых этими уравнениями.

Как отмечалось в §1.2, чтобы пол­ностью описать тот или иной физический процесс, необходимо, кроме самого урав­нения, описывающего этот процесс, за­дать начальное состояние этого процесса (начальные условия) и режим на границе той области, в которой происходит этот процесс (граничные условия). Математически это связанно с неединственностью решения дифференциальных уравнений. Действительно, даже для обыкновенных дифференциальных уравнений n -го порядка общее решение зависит от n произволь­ных постоянных. Для уравнений же в частных производных решение, вообще говоря, зависит от произвольных функций; например, общее решение уравнения 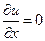в классе функций, зависящих от двух переменных x, y имеет вид u(x,y)=f(y), где f - произвольная функция класса С². Поэтому чтобы выделить решение, описывающее реальный физический процесс, необходимо задавать дополнительные условия. Такими дополнительными условиями и являются краевые условия: начальные и граничные условия. Соответствующая задача называется краевой задачей. Различают, таким образом, следующие три основных тина краевых задач для дифференциальных уравнений.

а) Задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область G совпадает со всем пространством Rⁿ, граничные условия отсутствуют.

б) Краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S, начальные условия, естественно, отсутствуют.

в) Смешанная задача для уравнений гиперболического и па­раболического типов: задаются и начальные, и граничные условия,

G¹Rⁿ

Опишем подробнее постановку каждой из перечисленных краевых задач для рассматриваемых уравнений (1.89) – (1.91).

 

2. Задача Коши. Для уравнения колебаний (1.89) (гиперболи­ческий тип) задача Коши ставится следующим образом: найти функ­цию u(x,t) класса C²(t > 0) Ç C^l(t ³0), удовлетворяющую уравне­нию (1.89) в полупространстве t > 0 и начальным условиям при

t = +0

(1.92)

При этом необходимо, чтобы FÎC(t > 0), u₀ÎС¹(Rⁿ), u₁ÎС(Rⁿ).

Для уравнения диффузии (1.90) (параболический тип) задача Коши ставится так: найти функцию u(x,t) класса С²(t > 0)Ç C(t ³ 0), удов­летворяющую уравнению (1.90) в полупространстве t > 0 и начальному условию при t = +0

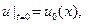(1.93)

При этом необходимо, чтобы FÎC(t > 0), u₀ÎС(Rⁿ),

Приведенная постановка задачи Коши допускает следующее обобщение. Даны квазилинейное дифференциальное уравнение вто­рого порядка гиперболического типа:

(1.94)

кусочно-гладкая поверхность S= {t= s(x)} и функции u₀ и u₁ на S (данные Коши). Задача Коши для уравнения (1.94) состоит в нахожде­нии решения u(x,t), определенного в некоторой части области t>s(x), примыкающей к поверхности S, и удовлетворяющего на S краевым условиям:

(1.95)

где n — нормаль к S, направленная в сторону возрастающих t (рис.9).

В задаче Коши (1.94), (1.95)важно, что поверхность S ни в одной точке не касается характеристической поверхности (см. §1.3, п. 3) уравнения (1.94). В противном случае задача Коши может или вовсе не иметь решения, или иметь неединственное решение.

Замечание. Решения поставленных краевых задач с гладкостью С¹ вплоть до границы области задания уравнения существуют не всегда. Поэтому иногда приходится отказываться от требования такой гладкости и требовать, например, чтобы решение было только непрерывным вплоть до границы области. Эта постановка является естественной в задачах, не содержащих первых производных в крае­вых условиях, например, для уравнений (1.90) и (1.91) с граничным услови­ем I рода. Если же в краевые условия входят первые производные, то в каждом конкретном случае необходимо указывать, в каком смысле должны быть выполнены эти краевые условия. Например, для сме­шанной задачи для уравнения (1.89) выполнения второго из начальных условий (1.92) можно требовать в смысле :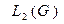

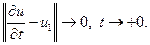(1.96)

Для задачи Неймана для уравнения Лапласа выполнения граничного условия (16) можно требовать в следующем смысле:

(1.97)

 

5. Другие краевые задачи. Сформулируем еще две краевые задачи, часто встречающиеся в математической физике.

а) Задача Гурса. Пусть дано линейное дифференциальное урав­нение гиперболического типа с двумя независимыми переменными в каноническом виде (см. § 1.3, п. 4):

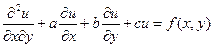(1.98)

с непрерывными коэффициентами a, b и с в замкнутом прямоугольнике:

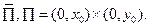
Требуется найти функцию и(х,у) класса 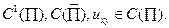удовлетворяющую уравнению (1.98) в прямоугольнике П и принимающую на его сторонах 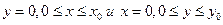(рис. 1.4) заданные значения:

(1.99)

 

Рис. 1.4

 

При этом должны быть выполнены условия гладкости:

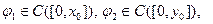
и условие согласованности

Отметим, что в задаче Гурса задается одно краевое условие ив двух пересекающихся характеристиках уравнения (1.98).

б) Задача Трикоми для уравнения Чаплыгина.

Уравнение Чап­лыгина имеет вид:

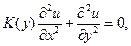(1.100)

где

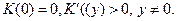
При 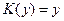уравнение (1.100) превращается в уравнение Трикоми (см. § 1.3, п. 5),

Рис. 1.5

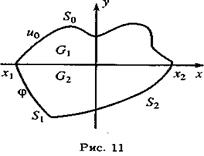
Пусть односвязная область G в плоскости (x, у) разделена параболической линией у = 0 уравнениями Трикоми на две части: эллиптическую G₁(y > 0) и гиперболическую G₂(y < 0). Предположим, что область g₁ в у > 0 ограничена кусочно-гладкой кривой So, которая оканчивается в точ­ках x₁ и х₂, х₁ < х₂, на оси x, a область G₂ в у < 0 ограничена двумя пересекающимися характеристиками S₁ и S₂ уравнения (1.100) (ср. §1.3, п. 5), проходящими соответственно через точки х₁ и x₂ на оси х (рис. 1.5).

Требуется найти функцию и(х,у) класса 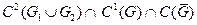удовлетворяющую уравнению (1.100) в областях g₁ и G₂ и принимающую на дуге So и на одной из характеристик, например, на S₁, заданные значения:

(1.101)

При этом необходимо, чтобы

 

6. Корректность постановок задач математической физики. Так как задачи математической физики представляют собой математические модели реальных физических процессов, то их постановки должны удовлетворять следующим естественным требованиям.

а) Решение должно существовать в каком-либо классе функций M₁.

б) Решение должно быть единственным в каком-либо классе функций М₂.

в) Решение должно непрерывно зависеть от данных задачи (на­чальных и граничных данных, свободного члена, коэффициентов уравнения и т. д.).

Непрерывная зависимость решения и от данных задачи D означает следующее: пусть последовательность данных D_k, k = 1,2,..., в каком-то смысле стремится к D, k → ∞, и и_k, k= 1,2,..., — соответствующие решения задачи; тогда должно быть u_k → u, k → ∞ в смысле надлежащим образом выбранной сходимости. Например, пусть задача приводится к уравнению Lu = F, где L — линейный оператор, переводящий М в N, где М и N — линейные нормированные пространства. В этом случае непрерывная зависимость решения и от свободного члена F будет обеспечена, если оператор L-^l существует и ограничен из N в М (см. §1.1, пп.8,9). Требование непрерывной зависимости решения обусловливается тем обстоятельством, что физические данные, как правило, определяются из эксперимента приближению, и поэтому нужно быть уверенным в том, что решение задачи в рамках выбранной математической модели не будет существенно зависеть от погрешностей измерений.

Задача, удовлетворяющая перечисленным требованиям, называется корректно поставленной (по Адамару), а множество функций M₁∩M₂ называется классом корректности. Задача, не удовлетворяющая хотя бы одному из условий а) - в), называется некорректно поставленной.

К некорректно поставленным задачам часто приводят обратные задачи математической физики: по некоторой информации о решение прямой задачи восстановить некоторые неизвестные физические величины, определяющие эту задачу (источники, краевые условия, коэффициенты уравнения и т.д.).

 

 

Примеры краевых задач