Термодинамика [4] основана на двух фундаментальных законах: первом законе термодинамики, или законе сохранения энергии, и втором законе термодинамики, или законе энтропии. Последовательная макроскопическая схема описания неравновесного процесса (т. е. схема термодинамики необратимого процесса) также должна быть построена на этих двух законах. Однако необходимо сформулировать эти законы в несколько иной, чем обычно, форме, которая соответствует нашим целям.
В настоящей главе мы рассмотрим первый закон термодинамики. Поскольку наша цель — развить теорию в применении к системам, свойства которых являются непрерывными функциями пространственных координат и времени, мы дадим локальную формулировку закона сохранения энергии. Так как локальные плотности импульса и массы могут изменяться во времени, нам потребуются также локальные формулировки законов сохранения импульса и массы.
Закон сохранения массы.
Рассмотрим систему, состоящую из n компонентов, между которыми возможны r химических реакций.
Скорость изменения массы компонента k в данном объеме V выражается формулой
(1.1)
где 
— плотность (т. е. масса единицы объема) компонента k. Эта величина равна сумме потока массы компонента k в объем V через его поверхность 
и полного образования k в химических реакциях, протекающих внутри объема V:
(1.2)
где d —вектор, равный по абсолютной величине d и направленный по нормали к поверхности, причем положительным направлением считается направление из объема наружу. Далее, 
есть скорость компонента k, а 
— образование компонента k на единицу объема в j-й химической реакции. Величина 
, деленная на молекулярную массу 
компонента k, пропорциональна стехиометрическому коэффициенту, с которым входит k в уравнение j-й химической реакции. Коэффициенты считаются положительными, когда компоненты k входят в правую часть, и отрицательными, когда они входят в левую часть уравнения реакции. Величина Jj- называется скоростью J'-й химической реакции. Она имеет размерность массы на единицу объема в единицу времени. Величины и Jj, входящие в (1.2), являются функциями времени и пространственных координат.
Применяя теорему Гаусса к поверхностному интегралу в (1.2), получаем
(k=1, 2…, n), (1.3)
поскольку соотношение (1.2) справедливо для произвольного объема V. Полученное уравнение имеет форму уравнения баланса: локальное изменение левой части равно дивергенции потока k, взятой с обратным знаком, и члену типа источника, выражающему образование (или уничтожение) вещества k.
Поскольку б каждой отдельной химической реакции масса сохраняется, мы получаем
(j=1, 2, …, r). (1.4)
Суммируя уравнение (1.3) по всем компонентам k, получаем закон сохранения массы
(1.5)
где 
— полная плотность
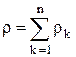(1.6)
a v—скорость центра масс элемента жидкости, т. е. массовая скорость
(1.7)
Уравнение (1.5) отражает сохранение полной массы, т. е. тот факт, что полная масса в элементе объема системы может измениться только в том случае, когда вещество втекает в элемент объема или вытекает из него.
Уравнение сохранения массы можно записать и в другом виде, если ввести полные производные по времени
(1.8)
и «диффузионный поток» вещества k, определяемый относительно движения центра масс
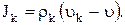(1.9)
При помощи (1.8) и (1.9) уравнение (1.3) можно записать в виде
(k=1, 2, …, n), (1.10)
а уравнение (2.5)—в виде
(1.11)
Если ввести концентрацию массы k-го компонента ck
(1.12)
то уравнение (2.10) принимает простую форму:
(k=1, 2, …, n). (1.13)
где было использовано также уравнение (1.11).
Вводя удельный объем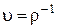 
, можно записать уравнение (1.11) в виде
(1.14)
Из (1.7) и (1.9), очевидно, следует, что
; (1.15)
таким образом, только n—1 из n диффузионных потоков являются независимыми. Аналогично независимы только n—1 из n уравнений (1.13). Действительно, суммируя (1.13) по всем k, находим, что обе части уравнения обращаются в нуль в силу соотношений (1.4), (1.12) и (1.15). Уравнение (1.14) является тогда n-м независимым уравнением, описывающим изменение плотности массы внутри системы.
Заметим, наконец, что для произвольной локальной величины а (которая может быть либо скаляром, либо компонентой вектора или тензора) справедливо уравнение
(1.16)
оно является следствием уравнения сохранения массы (1.5) и соотношения (1.8).
Уравнение движения
Уравнение движения системы имеет вид
(α=1, 2, 3), (1.17)
где 
(
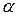=l, 2, 3)—декартовы компоненты скорости 
, α, 
(α ==1, 2, 3)—декартовы координаты. Производная dvα/dt является компонентой ускорения при движении центра инерции.
Величины Р 
(
=1, 2, 3) являются декартовыми компонентами тензора давлений (или напряжений) P среды, величины 
(α==1, 2, 3)—декартовыми координатами силы Fk, действующей на единицу массы компонента k. Примем здесь, что тензор давлений Р симметричен:
( =1, 2, 3). (1.18)
Такое предположение обычно делается в гидродинамике, но строго оно может быть обосновано только для систем, состоящих из сферических молекул, или при очень малых плотностях.
В тензорных обозначениях уравнение (1.17) запишется в виде
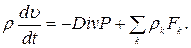(1.19)
Если исходить из рассмотрения микроскопических процессов, то можно сказать, что тензор давлений Р обусловлен короткодействующими взаимодействиями между частицами системы, тогда как Fk включает внешние силы, а также возможный вклад дальнодействующих взаимодействий в системе.
Закон сохранения энергии
Согласно закону сохранения энергии, полное количество энергии, содержащейся в некотором произвольном объеме V, может измениться только в том случае, если энергия втекает в объем (или вытекает из него) поверхность :
. (1.20)
Здесь e—энергия на единицу массы, а Je —поток энергии на единицу поверхности и в единицу времени. Мы будем называть величину е полной удельной энергией, так как она включает все возможные формы энергии системы. Аналогично назовем Je полным потоком энергии. При помощи теоремы Гаусса получаем дифференциальную, или локальную, форму закона сохранения энергии:
(1.21)
Определим различные вклады кинетической и потенциальной энергии е в поток Je
Полная удельная энергия е складывается из удельной кинетической энергии ½ 
, удельной потенциальной энергии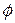 
и удельной внутренней энергии и.
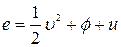(1.22)
С макроскопической точки зрения это соотношение можно рассматривать как определение понятия внутренней энергии и. С микроскопической точки зрения и представляет собой энергию теплового движения, а также энергию короткодействующих молекулярных взаимодействий. Аналогично полный поток энергии складывается из конвективного члена pev, потока энергии Р • v, обусловленного механической работой, совершенной над системой, потока потенциальной энергии 
, возникающего вследствие диффузии различных компонент в поле сил, и, наконец, «потока тепла» Jq:
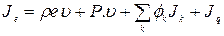(1.23)
Закон сохранения энтропии
Для открытых систем, т. е. систем, которые могут обмениваться с окружающей средой как тепловой энергией, так и веществом, deS - содержит член, связанный с передачей вещества. Теорема Карно—Клаузиуса [5] к таким системам неприменима. Однако общие утверждения равновесной термодинамики, остаются справедливыми. Заметим здесь, что в прикладных задачах равновесной термодинамики исследуются обратимые превращения. Наоборот, в неравновесной термодинамике одна из главных задач состоит в том, чтобы связать производство энтропии diS с различными необратимыми процессами, протекающими в системе. Прежде чем выразить производство энтропии через величины, характеризующие необратимые процессы, перепишем выражения для энтропии в форме, более удобной для описания системы, в которой плотности экстенсивных свойств (таких, как масса и энергия) являются непрерывными функциями пространственных координат. Запишем:
(1.24)
(1.25)
(1.26)
где s—энтропия на единицу массы, Js,полн — полный поток энтропии на единицу поверхности в единицу времени, а 
— интенсивность источника энтропии, или производство энтропии на единицу объема в единицу времени.
Используя (1.24) — (1.26) и теорему Гаусса, мы можем переписать закон сохранения энтропии в форме:
(1.27)
Поскольку основные законы термодинамики справедливы для произвольного объема V, из этого соотношения следует, что
(1.28)
(1.29)
Эти две формулы представляют собой локальную формулировку соотношений (3.1) и (3.2), т. е. локальное математическое выражение второго закона термодинамики. Уравнение (1.28) формально имеет вид уравнения баланса для плотности энтропии ps при наличии источника с интенсивностью , которая удовлетворяет важному соотношению (1.29). С помощью (1.16) уравнение (1.28) может быть переписано в несколько иной форме:
(1.30)
где поток энтропии Js представляет собой разность между полным потоком энтропии Js,полн и конвективным членом psυ:
(1.31)
При выводе (1.28) и (1.29) мы предполагали, что соотношения (3.l) и (3.2) справедливы и для бесконечно малых частей системы, или, иными словами, что законы, справедливые для макроскопических систем, остаются справедливыми и в применении к бесконечно малым частям этих систем. Такое предположение находится в согласии с обычной точкой зрения, которую принимают при макроскопическом описании непрерывных систем. Согласно этой точке зрения, локальные макроскопические измерения в системе действительно являются измерениями свойств малых частей системы, содержащих, однако, большое число составляющих систему частиц. Такие малые части системы можно назвать физически бесконечно малыми. Имея в виду что обстоятельство, мы можем говорить о локальных значениях таких существенно макроскопических понятий, как энтропия или производство энтропии.
Уравнение баланса энтропии
Теперь мы должны связать вариации свойств системы, со скоростью изменения энтропии. Это даст нам возможность получить явные выражения для входящих в уравнение (312) потока энтропии Js и интенсивности источника энтропии .
Из термодинамики мы знаем, что энтропия s на единицу массы для равновесной системы является вполне определенной функцией различных параметров, необходимых для полного описания макроскопического состояния системы. Такими параметрами являются внутренняя энергия и, удельный объем v и массовая концентрация сk:
(1.32)
Эго же свойство систем выражается тем фактом, что для системы, находящейся в равновесии, полный дифференциал s дается формулой Гиббса (см. приложение II):
(1.33)
где p—равновесное давление, a 
—термодинамический, или химический, потенциал компонента k (парциальная удельная функция Гиббса).
Примем теперь, что хотя полная система и не находится в равновесном состоянии, тем не менее в ней существуют малые элементы массы, которые находятся в состоянии «локального» равновесия и для которых локальная энтропия s является той же самой функцией (1.32) величин и. v и сk что и в состоянии полного равновесия. В частности, примем, что формула (1.33) остается справедливой для элемента массы вдоль пути его центра масс
(1.34)
где производные по времени даются формулой (2.8). Эта гипотеза о „локальном" равновесии с макроскопической точки зрения может быть оправдана только справедливостью получаемых с ее помощью выводов. Для специальных микроскопических моделей можно показать, что уравнение (1.34) справедливо, когда отклонения от равновесия, не слишком велики". С помощью этих микроскопических моделей можно также оценить, насколько большими могут быть отклонения от равновесия, чтобы уравнение (1.34) оставалось справедливым. К этому вопросу мы вернемся в гл. VII и IX, а здесь укажем, что для большинства известных явлений переноса использование соотношения (1.34) является оправданным.
Можно получить явную форму для уравнения баланса энтропии (1.30):
(1.35)
Однако, как видно из этого выражения, данное уравнение имеет тензорную форму, плохо применимо в реальных расчетах и делает уравнения, выведенные на основе этого закона, не решаемыми даже численно, из-за принципиальных трудностей, связанных с особенностями математических вычислений. Поэтому, в дальнейшем, для расчетов мы сформулирует первое фундаментальное приближение, которое всегда выполняется в практических технологических оценках и расчетах, и не требует специальных обоснований.
